Ramanujan's Papers
On certain arithmetical functions
Transactions of the Cambridge Philosophical Society, XXII,
No.9, 1916, 159 – 184
1. Let $\sigma_s(n)$ denote the sum of the $s$th powers of the divisors of $n$
(including 1 and $n$), and let
$$ \sigma_s (0) = \half \zeta (-s),$$
where $\zeta(s)$ is the Riemann Zeta-function. Further let
\begin{equation}
\sum_{r,s} (n) = \sigma_r (0) \sigma_s (n) + \sigma_r (1) \sigma_s(n-1) +
\cdots + \sigma_r (n) \sigma_s (0).
\end{equation}
In this paper I prove that
\begin{eqnarray}
\sum_{r,s} (n) &&= \frac{\Gamma (r+1) \Gamma (s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1) \zeta(s+1)}{\zeta(r+s+2)} \sigma_{r+s+1} (n) \nonumber \\
&&+ \frac{\zeta(1-r)+\zeta(1-s)}{r+s} n \sigma_{r+s-1} (n) + O \{n^{\frac{2}{3}
(r+s+1)}\},
\end{eqnarray}
whenever $r$ and $s$ are positive odd integers. I also prove that there is no
error term on the right-hand side of (2) in the following nine cases $r=1,
s=1; r=1, s=3; r=1, s=5; r=1, s=7; r=1, s=11, r=3, s=3; r=3, s=5; r=3,, s=9;
r=5, s=7.$ That is to say $\sum_{r,s} (n)$ has a finite expression in terms of
$\sigma_{r+s+1} (n)$ and $\sigma_{r+s-1} (n)$ in these nine cases; but for
other values of $r$ and $s$ it involves other arithmetical functions as well.
It appears probable, from the empirical results I obtain in $\S\S$ 18-23, that
the error term on the right-hand side of (2) is of the form
\begin{equation}
O \{ n^{\frac{1}{2}(r+s+1+\epsilon)} \},
\end{equation}
where $\epsilon$ is any positive number, and not of the form
\begin{equation}
o \{ n^{\frac{1}{2}(r+s+1)} \}.
\end{equation}
But all I can prove rigorously is (i) that the error is of the form
$$ O \{ n^{\frac{2}{3}(r+s+1)} \} $$
in all cases, (ii) that it is of the form
\begin{equation}
O \{ n^{\frac{2}{3}(r+s+\frac{3}{4})} \}
\end{equation}
if $r+s$ is of the form $6m$, (iii) that it is of the form
\begin{equation}
O \{ n^{\frac{2}{3}(r+s+\frac{1}{2})} \}
\end{equation}
if $r+s$ is of the form $6m + 4$, and (iv) that it is not of the form
\begin{equation}
o \{ n^{\frac{1}{2} (r+s)} \}.
\end{equation}
It follows from
(2) that, if $r$ and $s$ are positive odd integers, then
\begin{equation}
\sum_{r,s} (n) \sim \frac{\Gamma (r+1) \Gamma(s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1)\zeta(s+1)}{\zeta(r+s+2)} \sigma_{r+s+1} (n).
\end{equation}
It seems very likely that
(8) is true for all positive values of $r$ and $s$,
but this I am at present unable to prove.
2. If $\sum_{r,s} (n) / \sigma_{r+s+1} (n)$ tends to a limit, then the limit
must be
$$ \frac{\Gamma (r+1) \Gamma(s+1)}{\Gamma (r+s+2)}
\frac{\zeta(r+1)\zeta(s+1)}{\zeta(r+s+2)}.$$
For then
\begin{eqnarray*}
\lim_{n \to \infty} \frac{\sum_{r,s}(n)}{\sigma_{r+s+1}(n)} &=& \lim_{n \to
\infty} \frac{\sum_{r,s}(1) + \sum_{r,s} (2) + \cdots + \sum_{r,s} (n)}
{\sigma_{r+s+1} (1) + \sigma_{r+s+1} (2) + \cdots + \sigma_{r+s+1}(n)} \\
&=& \lim_{x \to 1} \frac{\sum_{r,s} (0) + \sum_{r,s} (1) x + \sum_{r,s} (2) x^2
+ \cdots}{\sigma_{r+s+1} (0) + \sigma_{r+s+1}(1) x + \sigma_{r+s+1} (2) x^2 +
\cdots}\\
&=& \lim_{x\to 1} \frac{S_r S_s}{S_{r+s+1}},
\end{eqnarray*}
where
\begin{equation}
S_r = \half \zeta(-r) + \frac{1^r x}{1-x} + \frac{2^r x^2}{1-x^2} +
\frac{3^r x^3}{1-x^3} + \cdots
\end{equation}
Now it is known that, if $r>0$, then
\begin{equation}
S_r \sim \frac{\Gamma (r+1) \zeta(r+1)}{(1-x)^{r+1}},
\end{equation}
as $x \to 1$
1.
Hence we obtain the result stated.
3. It is easy to see that
\begin{eqnarray*}
\sigma_r (1) + \sigma_r (2) + \sigma_r (3) + \cdots + \sigma_r (n) \\
= u_1 + u_2 + u_3 + u_4 + \cdots + u_n ,
\end{eqnarray*}
where
$$ u_t = 1^r + 2^r + 3^r + \cdots + \left[\frac{n}{t}\right]^r.$$
From this it is easy to deduce that
\begin{equation}
\sigma_r (1) + \sigma_r (2) + \cdots + \sigma_r (n) \sim
\frac{n^{r+1}}{r+1} \zeta (r+1)\href{#p18_en2}{^2}
\end{equation}
and
\begin{eqnarray*}
\sigma_r (1) (n-1)^s + \sigma_r (2) (n-2)^s + \cdots
+ \sigma_r (n-1) 1^s \sim \frac{\Gamma(r+1) \Gamma (s+1)}{\Gamma(r+s+2)}
\zeta(r+1)n^{r+s+1} ,
\end{eqnarray*}
provided $r \gt 0, s \geq0.$ Now
$$ \sigma_s (n) \gt n^s,$$
and
$$ \sigma_s (n) \lt n^s (1^{-s} + 2^{-s} + 3^{-s} + \cdots) = n^s \zeta (s).$$
From these inequalities and
(1) it follows that
\begin{equation}
\underline{\lim} \frac{\sum_{r,s} (n)}{n^{r+s+1}} \geq \frac{\Gamma(r+1)
\Gamma(s+1)}{\Gamma (r+s+2)} \zeta(r+1),
\end{equation}
if $r>0$ and $s\geq 0$; and
\begin{equation}
\overline{\lim} \frac{\sum_{r,s} (n)}{n^{r+s+1}} \leq
\frac{\Gamma(r+1)\Gamma(s+1)}{\Gamma(r+s+2)} \zeta(r+1) \zeta(s),
\end{equation}
if $r \gt 0$ and $s \gt 1$. Thus $n^{-r-s-1} \sum_{r,s}(n)$ oscillates between
limits included in the interval
$$ \frac{\Gamma(r+1) \Gamma(s+1)}{\Gamma(r+s+2)} \zeta(r+1), \:
\frac{\Gamma(r+1) \Gamma(s+1)}{\Gamma(r+s+2)} \zeta(r+1) \zeta(s).$$
On the other hand $n^{-r-s-1} \sigma_{r+s+1} (n)$ oscillates between 1 and
$\zeta(r+s+1)$, assuming values as near as we please to either of these
limits. The formula
(8) shews that the actual limits of indetermination of
$n^{-r-s-1} \sum_{r,s}(n)$ are
\begin{eqnarray}
&& \frac{\Gamma(r+1) \Gamma(s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1) \zeta(s+1)}{\zeta(r+s+2)},\nonumber \\
&& \frac{\Gamma(r+1) \Gamma(s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1) \zeta(s+1)\zeta(r+s+1)}{\zeta(r+s+2)}.
\end{eqnarray}
Naturally
$$
\zeta{(r+1)} \lt \frac{\zeta(r+1) \zeta(s+1)}{\zeta(r+s+2)} \lt
\frac{\zeta(r+1) \zeta(s+1)\zeta(r+s+1)}{\zeta(r+s+2)}
\lt \zeta(r+1) \zeta(s). \href{#p18_en3}{^3}$$
What is remarkable about the formula
(8) is that it shews the asymptotic
equality of two functions neither of which itself increases in a regular
manner.
4. It is easy to see that, if $n$ is a positive integer, then
$$ \cot \half \theta \sin n \theta = 1+2 \cos \theta +
2 \cos 2 \theta + \cdots + 2 \cos (n-1) \theta + \cos n\theta.$$
Suppose now that
\begin{eqnarray*}
&& \left(\myfrac{1}{4} \cot \half \theta + \frac{x \sin \theta}{1-x} +
\frac{x^2 \sin 2 \theta}{1-x^2} + \frac{x^3 \sin 3 \theta}{1-x^3} + \cdots
\right)^2 \\
&&= ( \myfrac{1}{4} \cot \half \theta)^2 + C_0 + C_1 \cos \theta + C_2 \cos
2 \theta + C_3 \cos 3 \theta + \cdots,
\end{eqnarray*}
where $C_n$ is independent of $\theta$. Then we have
\begin{eqnarray}
C_0 &=& \half \left(\frac{x}{1-x} + \frac{x^2}{1-x^2} +
\frac{x^3}{1-x^3} + \cdots \right)\nonumber \\
&+& \half \left\{\left(\frac{x}{1-x}\right)^2 +
\left(\frac{x^2}{1-x^2}\right)^2 + \left(\frac{x^3}{1-x^3}\right)^2 + \cdots
\right\}\nonumber \\
&=& \half \left\{ \frac{x}{(1-x)^2} + \frac{x^2}{(1-x^2)^2} +
\frac{x^3}{(1-x^3)^2} + \cdots \right\}\nonumber \\
&=& \half \left\{ \frac{x}{1-x} + \frac{2x^2}{1-x^2} +
\frac{3x^3}{1-x^3} + \cdots \right\}.
\end{eqnarray}
Again
\begin{eqnarray*}
C_n &=& \half \frac{x^n}{1-x^n} + \frac{x^{n+1}}{1-x^{n+1}}
+\frac{x^{n+2}}{1-x^{n+2}} + \frac{x^{n+3}}{1-x^{n+3}} + \cdots \\
&+& \frac{x}{1-x} \cdot \frac{x^{n+1}}{1-x^{n+1}} + \frac{x^2}{1-x^2} \cdot
\frac{x^{n+2}}{1-x^{n+2}} + \frac{x^3}{1-x^3} \cdot \frac{x^{n+3}}{1-x^{n+3}}
+ \cdots \\
&-& \half \left\{\frac{x}{1-x} \cdot \frac{x^{n-1}}{1-x^{n-1}} +
\frac{x^2}{1-x^2} \cdot \frac{x^{n-2}}{1-x^{n-2}} + \cdots +
\frac{x^{n-1}}{1-x^{n-1}} \cdot \frac{x}{1-x}\right\}.
\end{eqnarray*}
Hence
\begin{eqnarray*}
\frac{C_n}{x^n} (1-x^n) &=& \half + \left(\frac{x}{1-x} -
\frac{x^{n+1}}{1-x^{n+1}} \right)+\left(\frac{x^2}{1-x^2} -
\frac{x^{n+2}}{1-x^{n+2}} \right)+\cdots \\
&-& \half \left\{\left( 1+ \frac{x}{1-x} +
\frac{x^{n-1}}{1-x^{n-1}}\right) +\left(1+ \frac{x^2}{1-x^2} +
\frac{x^{n-2}}{1-x^{n-2}}\right) \right.\\
&& \:\:\:\:\:\:\:\:\:\:\:\:\:+ \cdots + \left.\left(1 +
\frac{x^{n-1}}{1-x^{n-1}} + \frac{x}{1-x} \right) \right\}\\
&=& \frac{1}{1-x^n} - \frac{n}{2}.
\end{eqnarray*}
That is to say
\begin{equation}
C_n = \frac{x^n}{(1-x^n)^2} - \frac{nx^n}{2(1-x^n)}.
\end{equation}
It follows that
\begin{eqnarray}
&& \left(\myfrac{1}{4} \cot \half \theta + \frac{x \sin \theta}{1-x} +
\frac{x^2 \sin 2 \theta}{1-x^2} + \frac{x^3 \sin 3 \theta}{1-x^3} + \cdots
\right)^2 \nonumber \\
&& =\left(\myfrac{1}{4} \cot \half \theta \right)^2 + \frac{x \cos
\theta}{(1-x)^2} + \frac{x^2 \cos 2 \theta}{(1-x^2)^2} + \frac{x^3 \cos 3
\theta}{(1-x^3)^2} + \cdots \nonumber \\
&& +\half\left\{ \frac{x}{1-x} (1-\cos \theta) + \frac{2x^2}{1-x^2}
(1-\cos 2 \theta) +
\frac{3x^3}{1-x^3} (1- \cos 3 \theta) + \cdots \right\}.
\end{eqnarray}
Similarly, using the equation
\begin{equation*}
\cot^2 \half \theta (1-\cos n \theta) =
(2n-1) + 4 (n-1) \cos \theta + 4(n-2) \cos 2 \theta + \cdots
+ 4 \cos (n-1) \theta + \cos n \theta,
\end{equation*}
we can shew that
\begin{eqnarray}
&& \left\{ \myfrac{1}{8} \cot^2 \half \theta + \myfrac{1}{12} +
\frac{x}{1-x} (1-\cos \theta) + \frac{2x^2}{1-x^2} (1-\cos 2 \theta)+
\right.\nonumber \\
&& \left. \frac{3x^3}{1-x^3} (1-\cos 3 \theta) + \cdots \right\}^2 =
\left(\myfrac{1}{8} \cot^2 \half \theta + \myfrac{1}{12}\right)^2 \nonumber \\
&& +\myfrac{1}{12}
\left\{\frac{1^3 x}{1-x} (5 + \cos \theta) + \frac{2^3 x^2}{1-x^2}(5 + \cos 2
\theta) + \frac{3^3 x^3}{1-x^3} (5 + \cos 3 \theta) + \cdots \right\}.
\end{eqnarray}
For example, putting $\theta = \myfrac{2}{3} \pi$ and $\theta = \half \pi$
in
(17), we obtain
\begin{eqnarray}
&& \left(\myfrac{1}{6} + \frac{x}{1-x} - \frac{x^2}{1-x^2} + \frac{x^4}{1-x^4}
- \frac{x^5}{1-x^5} + \cdots \right)^2 \nonumber \\
&&= \myfrac{1}{36} + \myfrac{1}{3} \left(\frac{x}{1-x} + \frac{2x^2}{1-x^2} +
\frac{4x^4}{1-x^4} + \frac{5x^5}{1-x^5}+ \cdots \right),
\end{eqnarray}
where $1,2,4,5, \ldots$ are the natural numbers without the multiples of $3$; and
\begin{eqnarray}
&& \left(\myfrac{1}{4} + \frac{x}{1-x} - \frac{x^3}{1-x^3} + \frac{x^5}{1-x^5}
- \frac{x^7}{1-x^7} + \cdots \right)^2 \nonumber \\
&&= \myfrac{1}{16} + \half \left(\frac{x}{1-x} + \frac{2x^2}{1-x^2} +
\frac{3x^3}{1-x^3} + \frac{5x^5}{1-x^5} + \cdots \right),
\end{eqnarray}
where $1,2,3,5, \ldots $ are the natural numbers without the multiples of 4.
5. It follows from (18) that
\begin{eqnarray}
&& \left(\frac{1}{2 \theta^2} + \frac{\theta^2}{2!} S_3 -
\frac{\theta^4}{4!} S_5 + \frac{\theta^6}{6!} S_7 - \cdots \right)^2 \nonumber \\
&&= \frac{1}{4 \theta^4} + \half S_3 - \myfrac{1}{12}
\left(\frac{\theta^2}{2!} S_5 - \frac{\theta^4}{4!} S_7 + \frac{\theta^6}{6!}
S_9 - \cdots \right),
\end{eqnarray}
where $S_r$ is the same as in
(9). Equating the coefficients of $\theta^n$ in
both sides in
(21), we obtain
\begin{eqnarray}
\frac{(n-2)(n+5)}{12(n+1)(n+2)} && S_{n+3} = {n\choose 2} S_3 S_{n-1} +
{n\choose 4} S_5 S_{n-8} + \nonumber \\
&& {n\choose 6} S_7 S_{n-5} + \cdots + {n\choose{n-2}} S_{n-1} S_3,
\end{eqnarray}
where
$$ {n\choose r} = \frac{n!}{r! (n-r)!},$$
if $n$ is an even integer greater than 2.
Let us now suppose that
\begin{equation}
\Phi_{r,s} (x) = \sum^{m=\infty}_{m=1} \sum^{n=\infty}_{n=1} m^r n^s
x^{mn},
\end{equation}
so that
$$\Phi_{r,s} (x) = \Phi_{s,r} (x), $$
and
\begin{eqnarray}
\left.\begin{array}{lll} \Phi_{0,s} (x) &=& \ds\frac{1^s x}{1-x} +
\frac{2^sx^2}{1-x^2} + \frac{3^s x^3}{1-x^3} + \cdots = S_s - \half
\zeta(-s), \\
\Phi_{1,s} (x) &=& \ds\frac{1^s x}{(1-x)^2} + \frac{2^s x^2}{(1-x^2)^2}+\label{18m1}
\frac{3^sx^3}{(1-x^3)^2} + \cdots \end{array}\right\}.
\end{eqnarray}
Further let
\begin{eqnarray}
\left.\begin{array}{llll}
P &=& -24S_1 = 1 - 24 \left(\ds\frac{x}{1-x} + \frac{2x^2}{1-x^2} +
\frac{3x^3}{1-x^3} + \cdots \right),\href{#p18_en4}{^4} \\
Q &=& 240S_3 = 1 + 240 \left(\ds\frac{1^3x}{1-x} + \frac{2^3 x^2}{1-x^2} +
\frac{3^3 x^3}{1-x^3} + \cdots \right),\\
R &=& - 540 S_5 = 1 - 504 \left(\ds\frac{1^5 x}{1-x} + \frac{2^5 x^2}{1-x^2} +
\frac{3^5 x^3}{1-x^3} + \cdots \right) \end{array}\right\}.
\end{eqnarray}
The putting $n=4, 6, 8, \ldots$ in (22) we obtain the results contained in the
following table.
TABLE 1
$$\begin{array}{ll}
1. & 1 - 24 \Phi_{0,1} (x) = P. \\
2. & 1 + 240 \Phi_{0,3} (x) = Q. \\
3. & 1 - 504 \Phi_{0,5} (x) = R. \\
4. & 1 + 480 \Phi_{0,7} (x) = Q^2.\\
5. & 1 - 264 \Phi_{0,9} (x) = QR. \\
6. & 691 + 65520 \Phi_{0,11} (x) = 441 Q^3 + 250 R^2. \\
7. & 1 - 24 \Phi_{0,13} (x) = Q^2 R. \\
8. & 3617 + 16320 \Phi_{0,15} (x) = 1617 Q^4 + 2000 QR^2. \\
9. & 43867 - 28728 \Phi_{0,17} (x) = 38367 Q^3 R + 5500 R^3. \\
10.& 174611 + 13200 \Phi_{0,19} (x) = 53361 Q^5 + 121250 Q^2 R^2.\\
11.& 77683 - 552 \Phi_{0,21} (x) = 57183 Q^4 R + 20500 Q R^3.\\
12.& 236364091+ 131040 \Phi_{0,23} (x) = 49679091 Q^6 + 176400000 Q^3 R^2\\
& +10285000 R^4.\\
13.& 657931 - 24 \Phi_{0,25} (x) = 392931 Q^5 R + 265000 Q^2 R^3. \\
14.& 3392780147 + 6960 \Phi_{0,27} (x) = 489693897 Q^7 + 2507636250 Q^4 R^2\\
& +395450000 Q R^4.\\
15.& 1723168255201 - 171864 \Phi_{0,29} (x) = 815806500201 Q^6 R\\
& +881340705000 Q^3 R^3 + 26021050000 R^5. \\
16.& 7709321041217 + 32640 \Phi_{0,31} (x) = 764412173217 Q^8\\
& + 5323905468000 Q^5 R^2 + 1621003400000 Q^2 R^4.
\end{array}$$
In general
\begin{equation}
\half \zeta (-s) + \Phi_{0,s} (x) = \sum K_{m,n} Q^m R^n,
\end{equation}
where $K_{m,n}$ is a constant and $m$ and $n$ are positive integers (including
zero) satisfying the equation
$$ 4m + 6n = s+1. $$
This is easily proved by induction, using
(22).
6. Again from (17) we have
\begin{eqnarray}
&& \left(\frac{1}{2\theta} + \frac{\theta}{1!} S_1 - \frac{\theta^3}{3!} S_3 +
\frac{\theta^5}{5!} S_5 - \cdots \right)^2 \nonumber \\
= \frac{1}{4 \theta^2} + S_1 - \frac{\theta^2}{2!} \Phi_{1,2} (x) &&+
\frac{\theta^4}{4!} \Phi_{1,4} (x) - \frac{\theta^6}{6!} \Phi_{1,6} (x) +
\cdots \nonumber \\
&&+ \half \left(\frac{\theta^2}{2!} S_3 - \frac{\theta^4}{4!} S_5 +
\frac{\theta^6}{6!} S_7 - \cdots \right).
\end{eqnarray}
Equating the coefficients of $\theta^n$ in both sides in
(27) we obtain
\begin{eqnarray}
\frac{n+3}{2(n+1)} S_{n+1} - \Phi_{1,n} (x) = {n\choose 1} S_1 S_{n-1} +
{n\choose 3} S_3 S_{n-3}+ \nonumber \\
{n\choose 5} S_5 S_{n-5} + \cdots + {n\choose {n-1}} S_{n-1} S_1,
\end{eqnarray}
if $n$ is a positive even integer. From this we deduce the results contained
in Table II.
TABLE II
$$\begin{array}{ll}
1. & 288 \Phi_{1,2} (x) = Q - P^2 . \\
2. & 720 \Phi_{1,4} (x) = PQ - R . \\
3. & 1008 \Phi_{1,6} (x) = Q^2 - PR .\\
4. & 720 \Phi_{1,8} (x) = Q (PQ - R).\\
5. & 1584 \Phi_{1,10} (x) = 3Q^3 + 2R^2 - 5PQR .\\
6. & 65520 \Phi_{1,12} (x) = P(441 Q^3 + 250 R^2) - 691 Q^2 R .\\
7. & 144 \Phi_{1,14} (x) = Q (3Q^3 + 4R^2 - 7 PQR) .
\end{array}$$
In general
\begin{equation}
\Phi_{1,s} (x) = \sum K_{l,m,n} P^l Q^m R^n,
\end{equation}
where $l \leq 2$ and $2l + 4m + 6n = s+2$. This is easily proved by
induction, using
(28).
We have
\begin{eqnarray}
\left.\begin{array}{lll}
x \ds\frac{dP}{dx} & = - & 24 \Phi_{1,2} (x) = \ds\frac{P^2 - Q}{12}, \\
x \ds\frac{dQ}{dx} &= & 240 \Phi_{1,4} (x) = \ds\frac{PQ - R}{3}, \\
x \ds\frac{dR}{dx} &= -& 504 \Phi_{1,6} (x) = \ds\frac{PR - Q^2}{2}
\end{array}\right\}
\end{eqnarray}
Suppose now that $r \lt s$ and that $r+s$ is even. Then
\begin{equation}
\Phi_{r,s} (x)= \left(x \frac{d}{dx}\right)^r \Phi_{0,s-r} (x),
\end{equation}
and $\Phi_{0, s-r} (x)$ is a polynomial in $Q$ and $R$. Also
$$ x \frac{dP}{dx}, \: x \frac{dQ}{dx}, \: x \frac{dR}{dx} $$
are polynomials in $P, Q$ and $R$. Hence $\Phi_{r,s} (x)$ is a polynomial in
$P, Q$ and $R$. Thus we deduce the results contained in Table III.
TABLE III
$$\begin{array}{lll}
1. & 1728 \Phi_{2,3} (x) = 3 PQ - 2R - P^3.\\
2. & 1728 \Phi_{2,5} (x) = P^2 Q - 2PR + Q^2.\\
3. & 1728 \Phi_{2,7} (x) = 2PQ^2 - P^2 R - QR.\\
4. & 8640 \Phi_{2,9} (x) = 9 P^2 Q^2 - 18 PQR + 5Q^3 + 4R^2.\\
5. & 1728 \Phi_{2,11} (x) = 6PQ^3 - 5P^2 QR + 4PR^2 - 5Q^2R. \\
6. & 6912 \Phi_{3,4} (x) = 6P^2Q - 8PR + 3Q^2 - P^4.\\
7. & 3456 \Phi_{3,6} (x) = P^3Q - 3P^2R+ 3PQ^2 - QR. \\
8. & 5184 \Phi_{3,8} (x) = 6P^2 Q^2 - 2P^3 R - 6PQR + Q^3 + R^2.\\
9. & 20736 \Phi_{4,5} (x) = 15PQ^2 - 20P^2 R + 10 P^3 Q - 4QR - P^5.\\
10. & 41472 \Phi_{4,7}(x) = 7(P^4 Q - 4P^3 R + 6P^2 Q^2 - 4PQR) + 3Q^3 +
4R^2.
\end{array}$$
In general
\begin{equation}
\Phi_{r,s} (x) = \sum K_{l,m,n} P^l Q^m R^n,
\end{equation}
where $l-1$ does not exceed the smaller of $r$ and $s$ and
$$ 2l + 4m + 6n = r + s + 1.$$
The results contained in these three tables are of course really results in
the theory of elliptic functions. For example $Q$ and $R$ are substantially
the invariants $g_2$ and $g_3$, and the formulæ of Table I are equivalent to
the formulæ which express the coefficients in the series
$$ \wp (u) = \frac{1}{u^2} + \frac{g_2 u^2}{20} + \frac{g_3 u^4}{28} +
\frac{g_2^2 u^6}{1200} + \frac{3g_2 g_3 u^8}{6160} + \cdots $$
in terms of $g_2$ and $g_3$. The elementary proof of these formulæ given in
the preceding sections seems to be of some interest in itself.
8. In what follows we shall require to know the form of $\Phi_{1,s} (x)$ more
precisely than is shewn by the formula (29).
We have
\begin{equation}
\half \zeta (-s) + \Phi_{0,s} (x) = \sum K_{m,n} Q^m R^n ,
\end{equation}
where $s$ is an odd integer greater than 1 and $4m + 6n = s + 1.$ Also
\begin{equation}
x \frac{d}{dx} (Q^m R^n) = \left(\frac{m}{3} + \frac{n}{2}\right) PQ^m
R^n - \left(\frac{m}{3} Q^{m-1} R^{n+1} + \frac{n}{3} Q^{m+2}
R^{n-1}\right).
\end{equation}
Differentiating
(33) and using
(34) we obtain
\begin{equation}
\Phi_{1,s+1} (x) = \myfrac{1}{12} (s+1) P \{ \half \zeta (-s) +
\Phi_{0,s} (x) \} + \sum K_{m,n} Q^m R^n,
\end{equation}
where $s$ is an odd integer greater than 1 and $4m + 6n = s+3$. But when
$s=1$ we have
\begin{equation}
\Phi_{1,2} (x) = \frac{Q-P^2}{288}.
\end{equation}
9. Suppose now that
\begin{eqnarray}
&& F_{r,s} (x) = \{\half \zeta (-r) + \Phi_{0,r} (x) \} \{\half
\zeta (-s) + \Phi_{0,s} (x) \}\nonumber \\
&&- \frac{\zeta(1-r) + \zeta(1-s)}{r+s} \Phi_{1,r+s} (x) - \frac{\Gamma(r+1)
\Gamma(s+1)}{\Gamma(r+s+2)} \frac{\zeta(r+1)\zeta(s+1)}{\zeta(r+s+2)} \nonumber \\
&& \times \{\half \zeta(-r -s-1) + \Phi_{0,r+s+1} (x) \}.
\end{eqnarray}
Then it follows from
(33),
(35) and
(36) that, if $r$ and $s$ are positive odd
integers,
\begin{equation}
F_{r,s} (x) = \sum K_{m,n} Q^m R^n,
\end{equation}
where
$$ 4m + 6n = r + s + 2.$$
But it is easy to see, from the functional equation satisfied by $\zeta(s)$,
viz.
\begin{equation}
(2 \pi)^{-s} \Gamma (s) \zeta(s) \cos \half \pi s = \half
\zeta (1-s),
\end{equation}
that
\begin{equation}
F_{r,s} (0) = 0.
\end{equation}
Hence $Q^3 - R^2$ is a factor of the right-hand side in
(38), that is to say
\begin{equation}
F_{r,s} (x) = (Q^3 - R^2) \sum K_{m,n} Q^m R^n,
\end{equation}
where
$$ 4m + 6n = r + s - 10.$$
10. It is easy to deduce from (30) that
\begin{equation}
x \frac{d}{dx} \log (Q^3 - R^2) = P.
\end{equation}
But it is obvious that
\begin{equation}
P = x \frac{d}{dx} \log [ x \{(1-x) (1-x^2) (1-x^3) \cdots \}^{24}];
\end{equation}
and the coefficient of $x$ in $Q^3 - R^2 = 1728$. Hence
\begin{equation}
Q^3 - R^2 = 1728x \{(1-x) (1-x^2) (1-x^3) \cdots \}^{24}.
\end{equation}
But it is known that
\begin{equation}
\{(1-x) (1-x^2) (1-x^3) (1-x^4) \cdots \}^3 \\
= 1 - 3x + 5x^3 - 7x^6 + 9x^{10} - \cdots
\end{equation}
Hence
\begin{equation}
Q^3 - R^2 = 1728x (1-3x + 5x^3 - 7x^6 + \cdots)^8.
\end{equation}
The coefficient of $x^{\nu-1}$ in $1- 3x + 5x^3 - \cdots$ is numerically less
than $\sqrt{(8 \nu)}$, and the coefficient of $x^{\nu}$ in $Q^3 - R^2$ is
therefore numerically less than that of $x^{\nu}$ in
$$ 1728 x \{ \sqrt{(8 \nu)} (1 + x + x^3 + x^6 + \cdots )\}^8.$$
But
\begin{equation}
x(1 + x + x^3 + x^6 + \cdots)^8 = \frac{1^3 x}{1-x^2} + \frac{2^3
x^2}{1-x^4} + \frac{3^3 x^3}{1-x^6} + \cdots,
\end{equation}
and the coefficient of $x^\nu$ in the right-hand side is positive and less
than
$$ \nu^3 \left(\frac{1}{1^3} + \frac{1}{3^3} + \frac{1}{5^3} + \cdots
\right).$$
Hence the coefficient of $x^\nu$ in $Q^3 - R^2$ is of the form
$$ \nu^4 O (\nu^3) = O (\nu^7).$$
That is to say
\begin{equation}
Q^3 - R^2 = \sum O (\nu^7) x^\nu.
\end{equation}
Differentiating
(48) and using
(42) we obtain
\begin{equation}
P(Q^3 - R^2) = \sum O (\nu^8) x^{\nu}.
\end{equation}
Differentiating this again with respect to $x$ we have
$$ A (P^2 - Q) (Q^3 - R^2) + BQ (Q^3 - R^2) = \sum O (\nu^9) x^{\nu},$$
where $A$ and $B$ are constants. But
$$P^2 - Q = - 288 \Phi_{1,2} (x) = - 288 \left\{\frac{1^2 x}{(1-x)^2} +
\frac{2^2 x^2}{(1-x^2)^2} + \cdots \right\}, $$
and the coefficient of $x^\nu$ in the right-hand side is a constant multiple
of $\nu \sigma_1 (\nu)$. Hence
\begin{eqnarray*}
(P^2 - Q) (Q^3 - R^2) &=& \sum O \nu \sigma_1 (\nu) x^\nu \sum O (\nu^7)
x^\nu \\
&=& \sum O(\nu^8) \{\sigma_1 (1) + \sigma_1(2) + \cdots \\
&& + \sigma_1 (\nu) \} x^\nu = \sum O (\nu^{10}) x^\nu,
\end{eqnarray*}
and so
\begin{equation}
Q(Q^3 - R^2) = \sum O (\nu^{10}) x^\nu.
\end{equation}
Differentiating this again with respect to $x$ and using arguments similar to
those used above, we deduce
\begin{equation}
R(Q^3 - R^2) = \sum O (\nu^{12}) x^\nu.
\end{equation}
Suppose now that $m$ and $n$ are any two positive integers including zero,
and that $m + n$ is not zero. Then
\begin{eqnarray*}
Q^m R^n (Q^3 - R^2) &=& Q(Q^3 - R^2) Q^{m-1} R^n \\
&=& \sum O (\nu^{10}) x^\nu \{\sum O (\nu^3) x^\nu\}^{m-1} \{\sum O(\nu^5) x^\nu
\}^n\\
&=& \sum O(\nu^{10}) x^\nu \sum O (\nu^{4m-5}) x^\nu \sum O (\nu^{6n-1})
x^\nu \\
&=& \sum O (\nu^{4m + 6n+6}) x^\nu,
\end{eqnarray*}
If $m$ is not zero, Similarly we can shew that
\begin{eqnarray*}
Q^m R^n (Q^3 - R^2) &=& R(Q^3 - R^2) Q^m R^{n-1} \\
&=& \sum O(\nu^{4m + 6n + 6}) x^\nu,
\end{eqnarray*}
if $n$ is not zero. Therefore in any case
\begin{equation}
(Q^3 - R^2) Q^m R^n = \sum O (\nu^{4m + 6n + 6}) x^\nu.
\end{equation}
11. Now let $r$ and $s$ be any two positive odd integers including zero.
Then, when $r+s$ is equal to 2,4,6,8 or 12, there are no values of $m$ and $n$
satisfying the relation
$$ 4m + 6n = r+s - 10$$
in (41); consequently in these cases
\begin{equation}
F_{r,s} (x) = 0.
\end{equation}
When $r+s = 10, m$ and $n$ must both be zero, and this result does not apply;
but it follows from
(41) and
(48) that
\begin{equation}
F_{r,s} (x) = \sum O(\nu^7) x^\nu.
\end{equation}
And when $r+s \geq 14$ it follows from
(52) that
\begin{equation}
F_{r,s} (x) = \sum O (\nu^{r+s-4}) x^\nu.
\end{equation}
Equating the coefficients of $x^\nu$ in both sides in
(53),
(54) and
(55) we
obtain
\begin{equation}
\sum_{r,s} (n) = \frac{\Gamma (r+1) \Gamma(s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1) \zeta(s+1)}{\zeta(r+s+2)} \sigma_{r+s+1} (n) \\
+ \frac{\zeta(1-r) + \zeta(1-s)}{r+s} n \sigma_{r+s-1} (n) + E_{r,s} (n),
\end{equation}
where
\begin{eqnarray*}
E_{r,s} (n) = 0, &&r+s = 2, 4, 6, 8, 12; \\
E_{r,s} (n) =O (n^7),&& r + s = 10; \\
E_{r,s} (n) = O (n^{r+s-4}),&& r + s \geq 14.
\end{eqnarray*}
Since $\sigma_{r+s+1} (n)$ is of order $n^{r+s+1}$, it follows that in all
cases
\begin{equation}
\sum_{r,s}(n) \sim \frac{\Gamma (r+1) \Gamma(s+1)}{\Gamma(r+s+2)}
\frac{\zeta(r+1) \zeta(s+1)}{\zeta(r+s+2)} \sigma_{r+s+1} (n).
\end{equation}
The following table gives the values of $\sum_{r,s} (n)$ when $r+s =
2,4,6,8,12$.
TABLE IV
$$\begin{array}{ll}
1. & \sum_{1,1} (n) = \frac{5 \sigma_3 (n) - 6n \sigma_1 (n)}{12}.\\
&\\
2. & \sum_{1,3} (n) = \frac{7 \sigma_5 (n) - 10 n \sigma_3 (n)}{80}.\\
3. & \sum_{3,3} (n) = \frac{\sigma_7 (n)}{120}. \\
&\\
4. & \sum_{1,5} (n) = \frac{10 \sigma_7 (n) - 21 n \sigma_5(n)}{252}.\\
&\\
5. & \sum_{3,5} (n) = \frac{11 \sigma_9 (n)}{5040}.\\
&\\
6. & \sum_{1,7} (n) = \frac{11 \sigma_9 (n) - 30 n \sigma_7 (n)}{480}.\\
&\\
7. & \sum_{5,7} (n) = \frac{\sigma_{13} (n)}{10080}.\\
&\\
8. & \sum_{3,9} (n) = \frac{\sigma_{13} (n)}{2640}.\\
&\\
9. & \sum_{1,11}(n) = \frac{691 \sigma_{13}(n)-2730 n \sigma_{11}(n)}{65520}.
\end{array}$$
12. In this connection it may be interesting to note that
\begin{eqnarray}
\sigma_1 (1) \sigma_3 (n) + \sigma_1 (3) \sigma_3 (n-1) + \sigma_1 (5)
\sigma_3 (n-2) + \cdots\nonumber \\
+ \sigma_1 (2n+1) \sigma_3 (0) = \myfrac{1}{240} \sigma_5 (2n+1).
\end{eqnarray}
This formula may be deduced from the identity
\begin{eqnarray}
\frac{1^5 x}{1-x} + \frac{3^5 x^2}{1-x^3} + \frac{5^5 x^3}{1-x^5} +
\cdots \nonumber \\
= Q \left(\frac{x}{1-x} + \frac{3x^2}{1-x^3} + \frac{5x^3}{1-x^5} +
\cdots\right),
\end{eqnarray}
which can be proved by means of the theory of elliptic functions or by
elementary methods.
13. More precise results concerning the order of $E_{r,s}(n)$ can be deduced
from the theory of elliptic functions. Let
$$ x = q^2.$$
Then we have
\begin{eqnarray}
\left.\begin{array}{llll}
&Q&=& \phi^8 (q) \{1 - (kk')^2\} \\
&R&=& \phi^{12} (q) (k'^2 - k^2) \{1 + \half (kk')^2 \} \\
&&=& \phi^{12} (q) \{ 1 + \half (kk')^2 \} \sqrt{\{1 - (2kk')^2 \}}
\end{array}\right\},
\end{eqnarray}
where $\{\phi(q)= 1 + 2q + 2q^4 + 2q^9 + \cdots\}$
But, if $$f(q) = q^{\frac{1}{24}} (1-q) (1-q^2) (1-q^3) \cdots, $$
then we know that
\begin{eqnarray}
\left.\begin{array}{lll}
2^{\frac{1}{6}} f(q) &=& k^{\frac{1}{12}} k'^{\frac{1}{3}} \phi (q) \\
2^{\frac{1}{6}} f(-q) &=& (kk')^{\frac{1}{12}} \phi(q) \\
2^{\frac{1}{3}} f(q^2) &=& (kk')^{\frac{1}{6}} \phi (q) \\
2^{\frac{2}{3}} f(q^4) &=& k^{\frac{1}{3}} k'^{\frac{1}{12}} \phi(q)
\end{array}\right\}
\end{eqnarray}
It follows from
(41),
(60) and
(61) that, if $r+s$ is of the form $4m + 2$,
but not equal to 2 or to 6, then
\begin{equation}
F_{r,s} (q^2) = \frac{f^{4(r+s-4)}(-q)}{f^{2(r+s-10)} (q^2)}
\sum^{\frac{1}{4} (r+s-6)}_{1} K_n \frac{f^{24n}(q^2)}{f^{24n} (-q)},
\end{equation}
and if $r+s$ is of the form $4m$, but not equal to 4, 8 or 12, then
\begin{equation}
F_{r,s}(q^2) = \frac{f^{4(r+s-6)}(-q)}{f^{2(r+s-10)} (q^2)} \{f^8 (q) - 16
f^8 (q^4) \} \sum^{\frac{1}{4} (r+s-8)}_{1} K_n \frac{f^{24n}(q^2)}{f^{24n}
(-q)},
\end{equation}
when $K_n$ depends on $r$ and $s$ only. Hence it is easy to see that in all
cases $F_{r,s} (q^2)$ can be expressed as
\begin{eqnarray}
\sum K_{a,b,c,d,e,h,k} \{f^3 (-q)\}^a \left\{\frac{f^5
(-q)}{f^2(q^2)}\right\}^b && \left\{\frac{f^5 (q^2)}{f^2 (-q)}\right\}^c
&& \left\{\frac{f^5 (q)}{f^2(q^2)} f^3 (q) \right\}^d \nonumber \\
\times \left\{\frac{f^5(q^4)}{f^2(q^2)} f^3 (q^4)\right\}^e f^h (-q) f^k
(q^2),
\end{eqnarray}
where $a,b,c,d,e,h,k$ are zero or positive integers such that
\begin{eqnarray*}
a + b + c + 2 ( d + e) = [\myfrac{2}{3} ( r + s + 2)], \\
h + k = 2 (r + s + 2) - 3 [\myfrac{2}{3} ( r + s + 2)],
\end{eqnarray*}
and $[x]$ denotes as usual the greatest integer in $x$. But
\begin{eqnarray}
\left.\begin{array}{lll}
f(q) &=& q^{\frac{1^2}{24}} - q^{\frac{5^2}{24}} - q^{\frac{7^2}{24}} +
q^{\frac{11^2}{24}} + \cdots \\
f^3 (q) &=& q^{\frac{1^2}{8}} - 3q^{\frac{3^2}{8}} + 5q^{\frac{5^2}{8}} -
7q^{\frac{7^2}{8}} + \cdots \\
\frac{f^5(q)}{f^2(q^2)} &=& q^{\frac{1^2}{24}} - 5q^{\frac{5^2}{24}} +
7q^{\frac{7^2}{24}} - 11 q^{\frac{11^2}{24}} + \cdots \\
\frac{f^5(q^2)}{f^2(-q)} &=& q^{\frac{1^2}{3}} - 2q^{\frac{2^2}{3}} +
4q^{\frac{4^2}{3}} - 5q^{\frac{5^2}{3}} + \cdots \end{array}\right\},
\end{eqnarray}
where $1,2,4,5, \cdots$ are the natural numbers without the multiples of 3, and
$1,5,7,11, \cdots$ are the natural odd numbers without the multiples of 3.
Hence it is easy to see that
$$n^{-\frac{1}{2} (a+b+c)-d-e} E_{r,s} (n) $$
is not of higher order than the coefficient of $q^{2n}$ in
$$ \phi^{a} (q^{\frac{1}{8}}) \phi^b (q^{\frac{1}{24}}) \phi^c
(q^{\frac{1}{3}}) \{ \phi (q^{\frac{1}{24}}) \phi (q^{\frac{1}{8}})\}^d
\{\phi (q^{\frac{2}{3}}) \phi (q^{\frac{1}{2}}) \}^e \phi^h (q^{\frac{1}{24}}) \phi^k
(q^{\frac{1}{12}}), $$
or the coefficient of $q^{48 n}$ in
$$ \phi^{a+d} (q^3) \phi^{b+d+h} (q) \phi^c (q^8) \phi^e (q^{16}) \phi^e
(q^{12}) \phi^k (q^2).$$
But the coefficient of $q^\nu$ in $\phi^2 (q^2)$ cannot exceed that of $q^\nu$
in $\phi^2 (q)$, since
\begin{equation}
\phi^2 (q) + \phi^2 (-q) = 2 \phi^2 (q^2);
\end{equation}
and it is evident that the coefficient of $q^\nu$ in $\phi(q^{4\lambda})$ cannot
exceed that of $q^\nu$ in $\phi (q^\lambda)$. Hence it follows that
$$n^{-\frac{1}{2} [ \frac{2}{3} (r + s + 2)] } E_{r,s} (n) $$
is not of higher order than the coefficient of $q^{48 n}$ in
$$\phi^A (q) \phi^B (q^3) \phi^C (q^2),$$
where $A, B, C$ are zero or positive integers such that
$$ A + B + C = 2 (r + s + 2) - 2 [ \myfrac{2}{3} (r + s + 2 )],$$
and $C$ is 0 or 1.
Now, if $r + s \geq 14$, we have
$$ A + B+ C \geq 12,$$
and so
$$ A + B \geq 11.$$
Therefore one at least of $A$ and $B$ is greater than 5. But
\begin{equation}
\phi^6 (q) = \sum^\infty_0 O (\nu^2) q^{\nu}.\href{#p18_en5}{^5}
\end{equation}
Hence it is easily deduced that
\begin{equation}
\phi^A (q) \phi^B (q^3) \phi^C (q^2) = \sum O \{ \nu^{\frac{1}{2} (A + B
+ C) -1}\} q^\nu.
\end{equation}
It follows that
\begin{equation}
E_{r,s} (n) = O \{n^{r+s - \frac{1}{2} [ \frac{2}{3} (r+s-1)]} \},
\end{equation}
If $r + s \geq 14.$ We have already shewn in $\S$ 11 that, if $r + s = 10$,
then
\begin{equation}
E_{r,s} (n) = O (n^7).
\end{equation}
This agrees with
(69). Thus we see that in all cases
\begin{equation}
E_{r,s} (n) = O \{ n^{\frac{2}{3} (r+s+1)}\};
\end{equation}
and that, if $r+s$ is of the form $6m$, then
\begin{equation}
E_{r,s} (n) = O \{n^{\frac{2}{3} (r+s+ \frac{3}{4})}\},
\end{equation}
and if of the form $6m + 4$, then
\begin{equation}
E_{r,s} (n) = O\{ n^{\frac{2}{3}(r+s+\frac{1}{2})} \}.
\end{equation}
14. I shall now prove that the order of $E_{r,s} (n)$ is not less than that of
$n^{\frac{1}{2} (r+s)}$. In order to prove this result I shall follow the
method used by Messrs Hardy and Littlewood in their paper ``Some problems of
Diophantine approximation'' (II) 6.
Let
$$ q = e^{\pi i \tau}, q' = e^{\pi i T},$$
where
$$T = \frac{c + d \tau}{a + b \tau},$$
and
$$ad - bc = 1.$$
Also let
$$V = \frac{v}{a + b \tau}.$$
Then we have
\begin{equation}
\omega \sqrt{v} e^{\pi i b vV}\vartheta_1 (v, \tau) =
\sqrt{V}\vartheta_1 (V, T ),
\end{equation}
where $\omega$ is an eighth root of unity and
\begin{equation}
\vartheta_1 (v, \tau) = 2 \sin \pi v\cdot q^{\frac{1}{4}} \Pi^\infty_1 (1- q^{2n}) (1
- 2q^{2n} \cos 2 \pi v + q^{4n}).
\end{equation}
From
(75) we have
\begin{equation}
\log \vartheta_1 (v, \tau) = \log (2, \sin \pi v) + \myfrac{1}{4} \log q -
\sum^\infty_1 \frac{q^{2n} (1 + 2 \cos 2 n \pi v)}{n(1-q^{2n})}.
\end{equation}
It follows from
(74) and
(76) that
\begin{eqnarray}
&& \log \sin \pi v + \half \log v + \myfrac{1}{4} \log q + \log \omega -
\sum^\infty_1 \frac{q^{2n} (1 + 2 \cos 2 n \pi v)}{n(1-q^{2n})}\nonumber \\
&&= \log \sin \pi V + \half\log V + \myfrac{1}{4} \log q' - \pi i b v V -
\sum^\infty_1 \frac{q^{'2n} (1 + 2 \cos 2 n \pi V)}{n(1-q^{'2n})}.
\end{eqnarray}
Equating the coefficients of $v^{8+1}$ on the two sides of
(77), we obtain
\begin{eqnarray}
(a + b\tau)^{s+1} && \left\{\half \zeta (-s) + \frac{1^s q^2}{1-q^2} +
\frac{2^s q^4}{1-q^4} + \frac{3^s q^6}{1-q^6} + \cdots \right\}\nonumber \\
&&= \half \zeta (-s) + \frac{1^s q'^2}{1-q'^2} + \frac{2^s q'^4}{1-q'^4} +
\frac{3^s q'^6}{1-q'^6} + \cdots,
\end{eqnarray}
provided that $s$ is an odd integer greater than 1. If, in particular,we put
$s=3$ and $s=5$ in
(78) we obtain
\begin{eqnarray}
(a+b\tau)^4 && \left\{ 1 + 240 \left(\frac{1^3 q^2}{1-q^2} + \frac{2^3
q^4}{1-q^4} + \frac{3^3 q^6}{1-q^6} + \cdots \right)\right\} \nonumber \\
&&= \left\{1 + 240 \left(\frac{1^3 q'^2}{1-q'^2} + \frac{2^3 q'^4}{1-q'^4} +
\frac{3^3 q'^6}{1-q'^6} + \cdots \right) \right\},
\end{eqnarray}
and
\begin{eqnarray}
(a+b\tau)^6 && \left\{ 1 -504 \left(\frac{1^5 q^2}{1-q^2} + \frac{2^5
q^4}{1-q^4} + \frac{3^5 q^6}{1-q^6} + \cdots \right)\right\} \nonumber \\
&&= \left\{1 -504 \left(\frac{1^5 q'^2}{1-q'^2} + \frac{2^5 q'^4}{1-q'^4} +
\frac{3^5 q'^6}{1-q'^6} + \cdots \right) \right\}.
\end{eqnarray}
It follows from
(38),
(79) and
(80) that
\begin{equation}
(a+b \tau)^{r+s+2} F_{r,s} (q^2) = F_{r,s} (q'^2).
\end{equation}
It can easily be seen from
(56) and
(37) that
\begin{equation}
F_{r,s} (x) = \sum^\infty_1 E_{r,s} (n) x^n.
\end{equation}
Hence
\begin{equation}
(a + b \tau)^{r+s+2} \sum^\infty_1 E_{r,s} (n) q^{2n} = \sum^\infty_1
E_{r,s} (n) q'^{2n}.
\end{equation}
It is important to observe that
\begin{eqnarray}
E_{r,s}(1) &&= \frac{\zeta (- r) + \zeta(-s)}{2} - \frac{\zeta(1-r) +
\zeta(1-s)}{r+s} \nonumber \\
&&- \frac{\Gamma(r+1) \Gamma(s+1)}{\Gamma(r+s+2)} \frac{\zeta(r+1)
\zeta(s+1)}{\zeta(r+s+2)} \neq 0,
\end{eqnarray}
if $r+s$ is not equal to 2,4,6,8 or 12. This is easily proved by the help of
the equation
(39).
15. Now let
$$\tau = u + iy, t = e^{-\pi y} ( u \gt 0, y \gt 0, 0 \lt t \lt 1), $$
so that
$$ q = e^{\pi i u - \pi y} = t e^{\pi i u} ; $$
and let us suppose that $p_n / q_n$ is a convergent to
$$ u = \frac{1}{a_1}{{}\atop{+}} \frac{1}{a_2}{{}\atop{+}}\frac{1}{a_3}{{}\atop{+
\cdots}}, $$
so that
$$ \eta_n = p_{n-1} q_n - p_n q_{n-1} = \pm 1.$$
Further, let us suppose that
$$ a = p_n, b = - q_n,$$
$$ c = \eta_n p_{n-1}, d = -\eta_n q_{n-1},$$
so that
$$ad - bc = \eta_n^2 = 1.$$
Furthermore, let
$$ y = 1 / (q_n q'_{n+1}),$$
where
$$q'_{n+1} = a'_{n+1} q_n + q_{n-1},$$
and $a'_{n+1}$ is the complete quotient corresponding to $a_{n+1}$.
Then we have
\begin{equation}
|a + b \tau| = |p_n - q_n u - i q_n y| = \frac{| \pm 1 - i|}{q'_{n+1}} =
\frac{\sqrt{2}}{q'_{n+1}},
\end{equation}
and
$$|q'| = e^{-\pi \lambda}, $$
where
\begin{eqnarray}
\lambda = {\bf I} (T) &=& {\bf I} \left(\frac{c + d \tau}{a + b
\tau}\right) + {\bf I} \left\{\frac{d}{b} - \frac{1}{b(a+b \tau)} \right\} \nonumber \\
&=& \frac{y}{(1/q'_{n+1})^2 + qn^2 y^2} = \frac{q'_{n+1}}{2q_n},
\end{eqnarray}
and ${\bf I} (T)$ is the imaginary part of $T$. It follows from
(83),
(85)
and
(86) that
\begin{eqnarray}
&& \vert \sum^\infty_1 E_{r,s} (n) q^{2n}\vert =
\left(\frac{q'_{n+1}}{\sqrt{2}}\right)^{r+s+2} \vert \sum^\infty_1 E_{r,s} (n)
q'^{2n} \vert \nonumber \\
\geq \left(\frac{q'_{n+1}}{\sqrt{2}} \right)^{r+s+2} && \{ |E_{r,s} (1) | e^{- 2
\pi \lambda} - | E_{r,s} (2) e^{-4 \pi \lambda} - |E_{r,s} (3)| e^{-6 \pi
\lambda} - \cdots \}.
\end{eqnarray}
We can choose a number $\lambda_0$, depending only on $r$ and $s$, such that
$$ |E_{r,s} (1) | e^{-2 \pi \lambda} \gt 2 \{|E_{r,s} (2)| e^{-4 \pi \lambda} +
|E_{r,s} (3) | e^{-6 \pi \lambda} + \cdots \}$$
for $\lambda \geq \lambda_0$. Let us suppose $\lambda_0 > 10.$ Let us also
suppose that the continued fraction for $u$ satisfies the condition
\begin{equation}
4 \lambda_0 q_n > q'_{n+1} > 2 \lambda_0 q_n
\end{equation}
for an infinity of values of $n$. Then
\begin{equation}
\left| \sum^\infty_1 E_{r,s} (n) q^{2n} \right | \geq \half
|E_{r,s} (1)| \left(\frac{q'_{n+1}}{\sqrt{2}} \right)^{r+s+2} e^{-4 \pi
\lambda_0} > K(q'_{n+1})^{r+s+2},
\end{equation}
where $K$ depends on $r$ and $s$ only. Also
$$q_n q'_{n+1} = 1/y,$$
$$q'_{n+1} \gt \frac{1}{\sqrt{y}} = \sqrt{\left\{\frac{\pi}{\log(1/t)}\right\}}
\gt \frac{K}{\sqrt{(1-t)}}.$$
It follows that, if $u$ is an irrational number such that the condition
(88)
is satisfied for an infinity of values of $n$, then
\begin{equation}
\left| \sum^\infty_1 E_{r,s} (n) q^{2n} \right| > K (1-t)^{-\frac{1}{2}
(r+s+2)}
\end{equation}
for an infinity of values of $t$ tending to unity.
But if we had
$$E_{r,s} (n) = o \{n^{\frac{1}{2} (r+s)}\}$$
then we should have
$$ \vert \sum^\infty_1 E_{r,s} (n) q^{2n} \vert = o
\{(1-t)^{-\frac{1}{2}(r+s+2)} \},$$
which contradicts
(90). It follows that the error term in $\sum_{r,s} (n)$
is not of the form
\begin{equation}
o \{n^{\frac{1}{2} (r+s)} \}.
\end{equation}
The arithmetical function $\tau(n)$
16. We have seen that
$$E_{r,s} (n) = 0, $$
if $r+s$ is equal to 2,4,6,8, or 12. In these cases $\sum_{r,s} (n)$ has a
finite expression in terms of $\sigma_{r+s+1} (n)$ and $\sigma_{r+s-1} (n)$.
In other cases $\sum_{r,s} (n)$ involves other arithmetical functions as
well. The simplest of these is the function $\tau(n)$ defined by
\begin{equation}
\sum^\infty_1 \tau (n) x^n = x \{(1-x) (1-x^2) (1-x^3) \cdots\}^{24}.
\end{equation}
These cases arise when $r+s$ has one of the values 10, 14, 16, 18, 20 or 24.
Suppose that $r+s$ has one of these values. Then
$$ \frac{1728 \sum^\infty_1 E_{r,s} (n) x^n}{(Q^3 - R^2) E_{r,s} (1)}$$
is, by (41) and (82), equal to the corresponding one of the functions
$$ 1, Q , R, Q^2, QR, Q^2R.$$
In other words
\begin{eqnarray}
&& \sum^\infty_1 E_{r,s} (n) x^n = E_{r,s} (1) \sum^\infty_1 \tau (n) x^n
\nonumber \\
&& \left\{ 1 + \frac{2}{\zeta(11-r-s)} \sum^\infty_1 n^{r+s-11}
\frac{x^n}{1-x^n}\right\}.
\end{eqnarray}
We thus deduce the formulæ
\begin{equation}
E_{r,s} (n) = E_{r,s} (1) \tau (n),
\end{equation}
if $r+s=10$; and
\begin{eqnarray}
&& \sigma_{r+s-11} (0) E_{r,s} (n) = E_{r,s} (1) \{\sigma_{r+s-11} (0)
\tau(n) \nonumber \\
&& + \sigma_{r+s-11} (1) \tau (n-1) + \cdots + \sigma_{r+s-11} (n-1) \tau (1) \},
\end{eqnarray}
if $r+s$ is equal to 14, 16, 18, 20 or 24. It follows from
(94) and
(95)
that, if $r+s=r'+s'$, then
\begin{equation}
E_{r,s} (n) E_{r',s'} (1) = E_{r,s} (1) E_{r',s'} (n),
\end{equation}
and in general
\begin{equation}
E_{r,s} (m) E_{r',s'} (n) = E_{r,s} (n) E_{r',s'} (m),
\end{equation}
when $r+s$ has one of the values in question. The different cases in which
$r+s$ has the same value are therefore not fundamentally distinct.
17. The values of $\tau(n)$ may be calculated as follows: differentiating
(92) logarithmically with respect to $x$, we obtain
\begin{equation}
\sum^\infty_1 n \tau(n) x^n = P \sum^\infty_1 \tau (n) x^n.
\end{equation}
Equating the coefficients of $x^n$ in both sides in
(98),we have
\begin{equation}
\tau(n) = \frac{24}{1-n} \{\sigma_1 (1) \tau (n-1) + \sigma_1 (2) \tau
(n-2) + \cdots + \sigma_1 (n-1) \tau(1)\}.
\end{equation}
If, instead of starting with
(92), we start with
$$ \sum^\infty_1 \tau (n) x^n = x (1-3x + 5x^3 - 7x^6 + \cdots)^8, $$
we can shew that
\begin{eqnarray}
&& (n-1) \tau(n) - 3(n-10) \tau (n-1) + 5(n-28) \tau (n-3) - 7\nonumber \\
&& (n-55) \tau (n-6) + \cdots \:{\rm to}\: [\half \{1 + \sqrt{(8n-7)}\}]
\:{\rm terms}\: = 0,
\end{eqnarray}
where the $r$th term of the sequence 0,1,3,6, $\ldots$ is $\frac{1}{2} r(r-1)$, and
the $r$th term of the sequence 1,10,28,55, $\ldots$ is $1 + \frac{9}{2} r (r-1)$.
We thus obtain the values of $\tau(n)$ in the following table.
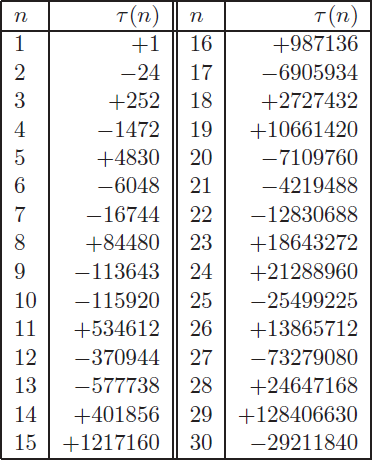
18. Let us consider more particularly the case in which $r+s=10$. The order
of $E_{r,s}(n)$ is then the same as that of $\tau(n)$. The determination of
this order is a problem interesting in itself. We have proved that $E_{r,s}
(n)$, and therefore $\tau(n)$, is of the form $O(n^7)$ and not of the form
$o(n^5)$. There is reason for supposing that $\tau(n)$ is of the form
$O(n^{\frac{11}{2}+\epsilon})$ and not of the form $o(n^{\frac{11}2}).$ For
it appears that
\begin{equation}
\sum^\infty_1 \frac{\tau(n)}{n^t} = \prod_p \frac{1}{1-\tau(p)p^{-t} +
p^{11-2t}}.
\end{equation}
This assertion is equivalent to the assertion that, if
$$ n = p_1^{a_1} p_2^{a_2} p_3^{a_3} \cdots p_r^{a_r}, $$
where $p_1, p_2, \ldots, p_r$ are the prime divisors of $n$, then
\begin{equation}
n^{-\frac{11}{2}} \tau(n) = \frac{\sin (1+a_1)\theta_{p_1} \sin
(1+a_2)\theta_{p_2}}{\sin \theta_{p_1} \sin \theta_{p_2}}
\cdots \frac{\sin(1+a_r)\theta_{p_r}}{\sin \theta_{p_r}},
\end{equation}
where
$$ \cos \theta_p = \half p^{-\frac{11}{2}} \tau(p).$$
It would follow that, if $n$ and $n'$ are prime to each other, we must have
\begin{equation}
\tau (nn') = \tau (n) \tau (n').
\end{equation}
Let us suppose that
(102) is true, and also that (as appears to be highly
probable)
\begin{equation}
\{2 \tau (p)\}^2 \leq p^{11},
\end{equation}
so that $\theta_p$ is real. Then it follows from
(102) that
$$n^{-\frac{11}{2}} |\tau (n)| \leq (1+a_1) (1+a_2) \cdots (1+a_r),$$
that is to say
\begin{equation}
|\tau (n) |\leq n^{\frac{11}{2}} d (n),
\end{equation}
where $d(n)$ denotes the number of divisors of $n$.
Now let us suppose that $n = p^a$, so that
$$n^{-\frac{11}{2}} \tau(n) = \frac{\sin(1+a)\theta_p}{\sin \theta_p}.$$
Then we can choose $a$ as large as we please and such that
$$ \left|\frac{\sin (1+a)\theta_p}{\sin \theta_p}\right| \geq 1.$$
Hence
\begin{equation}
|\tau(n) | \geq n^{\frac{11}{2}}
\end{equation}
for an infinity of values of $n$.
19. It should be observed that precisely similar questions arise with regard
to the arithmetical function $\Psi(n)$ defined by
\begin{equation}
\sum^\infty_0 \Psi (n) x^n = f^{a_1} (x^{c_1}) f^{a_2} (x^{c_2}) \cdots
f^{a_r} (x^{c_r}),
\end{equation}
where
$$ f(x) = x^{\frac{1}{24}} (1-x) (1-x^2) (1-x^3) \cdots,$$
the $a$'s and $c$'s are integers, the latter being positive,
$$\myfrac{1}{24} (a_1 c_1 - a_2 c_2 + \cdots + a_r c_r)$$
is equal to 0 or 1, and
$$l \left(\frac{a_1}{c_1} + \frac{a_2}{c_2} + \cdots
+\frac{a_r}{c_r}\right),$$
where $l$ is the least common multiple of $c_1, c_2, \ldots, c_r,$ is equal to
0 or to a divisor of 24.
The arithmetical functions $\chi(n), P(n), \chi_4 (n), \Omega(n)$ and
$\Theta(n)$, studied by Dr. Glaisher in the Quarterly Journal, Vols.
XXXVI-XXXVIII, are of this type. Thus
\begin{eqnarray*}
\sum^\infty_1 \chi (n)x^n &=& f^6(x^4), \\
\sum^\infty_1 P (n) x^n &=& f^4 (x^2) f^4(x^4), \\
\sum^\infty_1 \chi_4 (n) x^n &=& f^4(x) f^2(x^2) f^4(x^4), \\
\sum^\infty_1 \Omega (n) x^n &=& f^{12} (x^2), \\
\sum^\infty_1 \Theta (n) x^n &=& f^8 (x) f^8(x^2).
\end{eqnarray*}
20. The results (101) and (104) may be written as
\begin{equation}
\sum^\infty_1 \frac{E_{r,s}(n)}{n^t} = E_{r,s} (1) \prod_p \frac{1}{1-2c_p
p^{-t} + p^{r+s+1-2t}},
\end{equation}
where
$$c^2_p \leq p^{r+s+1}, $$
and
$$2c_p E_{r,s} (1) = E_{r,s} (p).$$
It seems probable that the result (108) is true not only for $r+s=10$ but also
when $r+s$ is equal to 14, 16, 18, 20 or 24, and that
\begin{equation}
\left|\frac{E_{r,s}(n)}{E_{r,s}(1)}\right| \leq n^{\frac{1}{2}(r+s+1)}
d(n)
\end{equation}
for all values of $n$, and
\begin{equation}
\left|\frac{E_{r,s}(n)}{E_{r,s}(1)}\right| \geq n^{\frac{1}{2}(r+s+1)}
\end{equation}
for an infinity of values of $n$. If this be so, then
\begin{equation}
E_{r,s} (n) = O \{n^{\frac{1}{2}(r+s+1+\epsilon)}\}, E_{r,s} (n) \neq o
\{n^{\frac{1}{2}(r+s+1)} \}.
\end{equation}
And it seems very likely that these equations hold generally, whenever $r$ and
$s$ are positive odd integers.
21. It is of some interest to see what confirmation of these conjectures can
be found from a study of the coefficients in the expansion of
$$x \{(1-x^{24/\alpha}) (1-x^{48/\alpha}) (1-x^{72/\alpha}) \cdots \}^a =
\sum^\infty_1 \Psi_\alpha (n) x^n,$$
where $\alpha$ is a divisor of 24. When $\alpha=1$ and $\alpha=3$ we know the
actual value of $\Psi_{\alpha} (n)$. For we have
\begin{equation}
\sum^\infty_1 \Psi_1 (n) x^n = x^{1^2} - x^{5^2} - x^{7^2} + x^{11^2} +
x^{13^2} - x^{17^2} - \cdots,
\end{equation}
where 1, 5, 7, 11, $\ldots$ the natural odd numbers without the multiples of 3; and
\begin{equation}
\sum^\infty_1 \Psi_3 (n) x^n = x^{1^2} - 3x^{3^2} + 5x^{5^2} - 7x^{7^2} +
\cdots
\end{equation}
The corresponding Dirichlet's series are
\begin{equation}
\sum^\infty_1 \frac{\Psi_1(n)}{n^s} = \frac{1}{(1+5^{-2s})(1+7^{-2s})
(1-11^{-2s})(1-13^{-2s})\cdots},
\end{equation}
where 5, 7, 11, 13,$\ldots$ are the primes greater than 3, those of the form $12n \pm
5$ having the plus sign and those of the form $12n \pm 1$ the minus sign; and
\begin{equation}
\sum^\infty_1\frac{\Psi_3(n)}{n^s} = \frac{1}{(1+3^{1-2s})
(1-5^{1-2s})(1+7^{1-2s}) (1+11^{1-2s})\cdots}
\end{equation}
where 3, 5, 7, 11, $\ldots$ are the odd primes, those of the form $4n-1$ having the
plus sign and those of the form $4n+1$ the minus sign.
It is easy to see that
\begin{equation}
|\Psi_1 (n) | \leq 1, ~~ |\Psi_3 (n) |\leq \sqrt{n}
\end{equation}
for all values of $n$, and
\begin{equation}
|\Psi_1 (n) | = 1, ~~ |\Psi_3 (n) | = \sqrt{n}
\end{equation}
for an infinity of values of $n$.
The next simplest case is that in which $\alpha = 2$. In this case it appears
that
\begin{equation}
\sum^\infty_1 \frac{\Psi_2(n)}{n^s} = \Pi_1 \Pi_2,
\end{equation}
where
$$ \Pi_1 = \frac{1}{(1+5^{-2s})(1-7^{-2s})(1-11^{-2s})(1+17^{-2s}) \cdots},$$
5, 7, 11, $\ldots$ being the primes of the forms $12n-1$ and $12n \pm 5$, those of the
form $12n + 5$ having the plus sign and the rest the minus sign; and
$$ \Pi_2 = \frac{1}{(1+13^{-s})^2(1-37^{-s})^2(1-61^{-s})^2 (1+73^{-s})^2
\cdots},$$
13, 37, 61, $\ldots$ being the primes of the form $12n+1$, those of the form
$m^2+(6n-3)^2$ having the plus sign and those of the form $m^2+(6n)^2$ the
minus sign.
This is equivalent to the assertion that if
$$n = (5^{a_5} \cdot 7^{a_7} \cdot 11^{a_{11}} \cdot 17^{a_{17}} \cdots)^2
13^{a_{13}} \cdot 37^{a_{37}} \cdot 61^{a_{61}} \cdot 73^{a_{73}} \cdots,$$
where $a_p$ is zero or a positive integer, then
\begin{equation}
\Psi_2(n) = (-1)^{a_5+ a_{13} + a_{17}+a_{29} + a_{41}+\cdots} (1+a_{13})
(1+a_{37}) (1+a_{61}) \cdots,
\end{equation}
where 5, 13, 17, 29, $\ldots$ are the primes of the form $4n + 1$, excluding those of
the form $m^2 + (6n)^2$; and that otherwise
\begin{equation}
\Psi_2 (n) = 0.
\end{equation}
It follows that
\begin{equation}
| \Psi_2(n) | \leq d(n)
\end{equation}
for all values of $n$, and
\begin{equation}
| \Psi_2 (n) | \geq 1
\end{equation}
for an infinity of values of $n$. These results are easily proved to be
actually true.
22. I have investigated also the cases in which $\alpha$ has one of the
values 4, 6, 8 or 12. Thus for example, when $\alpha=6$, I find
\begin{equation}
\sum^\infty_1 \frac{\Psi_6(n)}{n^s} = \Pi_1 \Pi_2,\href{#p18_en7}{^7}
\end{equation}
where
$$ \Pi_1 = \frac{1}{(1-3^{2-2s})(1-7^{2-2s})(1-11^{2-2s})\cdots},$$
3, 7, 11, $\ldots$ being the primes of the form $4n -1$; and
$$\Pi_2=\frac{1}{(1-2c_5\cdot 5^{-s}+5^{2-2s})(1-2c_{13}\cdot
13^{-s}+13^{2-2s})\cdots},$$
5, 13, 17, $\ldots$ being the primes of the form $4n +1$, and $c_p = u^2 - (2v)^2$,
where $u$ and $v$ are the unique pair of positive integers for which $p = u^2
+ (2v)^2$. This is equivalent to the assertion that if
$$ n = (3^{a_3} \cdot 7^{a_7} \cdot 11^{a_{11}} \cdots)^2 \cdot 5^{a_5} \cdot
13^{a_{13}} \cdot 17^{a_{17}} \cdots, $$
then
\begin{equation}
\frac{\Psi_6(n)}{n} = \frac{\sin(1+a_5)\theta_5}{\sin \theta_5} \cdot
\frac{\sin(1+a_{13})\theta_{13}}{\sin \theta_{13}} \cdot
\frac{\sin(1+a_{17})\theta_{17}}{\sin \theta_{17}} \cdots,
\end{equation}
where
$$ \tan \half \theta_p = \frac{u}{2v} \:\:\: (0 \lt \theta_p \lt \pi),$$
and that otherwise $\Psi_6(n)=0.$ From these results it would follow that
\begin{equation}
|\Psi_6(n) | \leq n d(n)
\end{equation}
for all values of $n$, and
\begin{equation}
|\Psi_6(n) | \geq n
\end{equation}
for an infinity of values of $n$. What can actually be proved to be true is
that
$$|\Psi_6(n) \lt 2 n d (n) $$
for all values of $n$, and
$$ |\Psi_6(n) | \geq n$$
for an infinity of values of $n$.
23. In the case in which $\alpha = 4$ I find that, if
$$ n = (5^{a_5} \cdot 11^{a_{11}} \cdot 17^{a_{17}} \cdots)^2 \cdot 7^{a_7}
\cdot 13^{a_{13}} \cdot 19^{a_{19}} \cdots, $$
where 5, 11, 17, $\ldots$ are the primes of the form $6m -1$
and 7, 13, 19, $\ldots$ are those of the form $6m +1$, then
\begin{equation}
\frac{\Psi_4(n)}{\sqrt{n}} = (-1)^{a_5 + a_{11} + a_{17}+\cdots}
\frac{\sin(1+a_7) \theta_7}{\sin \theta_7} \cdot
\frac{\sin(1+a_{13})\theta_{13}}{\sin \theta_{13}} \cdots,
\end{equation}
where
$$\tan \theta_p = \frac{u\sqrt{3}}{1 \pm 3 v} \:\:\: (0 \lt \theta_p \lt \pi),$$
and $u$ and $v$ are the unique pair of positive integers for which $p = 3u^2 +
(1 \pm 3v)^2$; and that $\Psi_4 (n) = 0$ for other values.
In the case in which $\alpha=8$ I find that, if
$$ n = (2^{a_2} \cdot 5^{a_5} \cdot 11^{a_{11}} \cdots)^2 \cdot 7^{a_7} \cdot
13^{a_{13}} \cdot 19^{a_{19}} \cdots, $$
where 2, 5, 11, $\ldots$ are the primes of the form $3m - 1$ and 7, 13, 19, $\ldots$
are those of the form $6m +1$, then
\begin{equation}
\frac{\Psi_8(n)}{n\sqrt{n}} = (-1)^{a_2+a_5 + a_{11} +\cdots}
\frac{\sin 3(1+a_7) \theta_7}{\sin 3 \theta_7} \cdot
\frac{\sin 3(1+a_{13})\theta_{13}}{\sin 3 \theta_{13}} \cdots,
\end{equation}
where $\theta_p$ is the same as in
(127); and that $\Psi_8 (n)=0$ for other
values.
The case in which $\alpha=12$ will be considered in $\S$ 28.
In short, such evidence as I have been able to find, while not conclusive,
points to the truth of the results conjectured in $\S$ 18.
24. Analysis similar to that of the preceding sections may be applied to some
interesting arithmetical functions of a different kind. Let
\begin{equation}
\phi^s (q) = 1 + 2 \sum^\infty_1 r_s (n) q^n,
\end{equation}
where
$$ \phi (q) = 1 + 2q + 2q^4 + 2q^9 + \cdots, $$
so that $r_s (n)$ is the number of representations of $n$ as the sum of $s$
squares. Further let
\begin{eqnarray}
\sum^\infty_1 \delta_2 (n) q^n &=& 2 \left(\frac{q}{1-q} -
\frac{q^3}{1-q^3} + \frac{q^5}{1-q^5} - \cdots \right) \nonumber \\
&=& 2 \left(\frac{q}{1+q^2}+ \frac{q^2}{1+q^4} + \frac{q^3}{1+q^6} + \cdots
\right);
\end{eqnarray}
\begin{equation}
(2^s - 1) B_s \sum^\infty_1 \delta_{2s} (n) q^n = s
\left(\frac{1^{s-1}q}{1+q} + \frac{2^{s-1}q^2}{1-q^2} +
\frac{3^{s-1}q^3}{1+q^3}
+ \cdots \right) ,
\end{equation}
when $s$ is a multiple of 4;
\begin{equation}
(2^s - 1) B_s \sum^\infty_1 \delta_{2s} (n) q^n = s
\left(\frac{1^{s-1}q}{1-q} + \frac{2^{s-1}q^2}{1+q^2} +
\frac{3^{s-1}q^3}{1-q^3} + \cdots \right),
\end{equation}
when $s+2$ is a multiple of 4;
\begin{eqnarray}
E_s \sum^\infty_1 \delta_{2s} (n)q^n &&= 2^s \left(\frac{1^{s-1}q}{1+q^2} +
\frac{2^{s-1}q^2}{1+q^4} + \frac{3^{s-1}q^3}{1+q^6} +
\cdots \right) \nonumber \\
&& +2 \left(\frac{1^{s-1}q}{1-q}
\frac{3^{s-1}q^3}{1-q^3} + \frac{5^{s-1}q^5}{1-q^5} - \cdots \right),
\end{eqnarray}
when $s-1$ is a multiple of 4;
\begin{eqnarray}
E_s \sum^\infty_1 \delta_{2s} (n)q^n = 2^s \left(\frac{1^{s-1}q}{1+q^2} +
\frac{2^{s-1}q^2}{1+q^4} + \frac{3^{s-1}q^3}{1+q^6} +
\cdots \right) \nonumber \\
-2 \left(\frac{1^{s-1}q}{1-q} -
\frac{3^{s-1}q^3}{1-q^3} + \frac{5^{s-1}q^5}{1-q^5} - \cdots \right),
\end{eqnarray}
when $s+1$ is a multiple of 4. In these formulæ
$$B_2 = \myfrac{1}{6}, B_4 = \myfrac{1}{30}, B_6 = \myfrac{1}{42}, B_8 =
\myfrac{1}{30}, B_{10} = \myfrac{5}{66}, \ldots $$
are Bernoulli's numbers, and
$$ E_1 = 1, E_3 = 1, E_5 = 5, E_7 = 61, E_9 = 1385, \ldots $$
are Euler's numbers. Then $\delta_{2s} (n)$ is in all cases an arithmetical
function depending on the real divisors of $n$; thus, for example, when $s+2$
is a multiple of 4, we have
\begin{equation}
(2^s -1) B_s \delta_{2s} (n) = s \{\sigma_{s-1} (n) - 2^s \sigma_{s-1}
(\myfrac{1}{4} n)\},
\end{equation}
where $\sigma_s (x)$ should be considered as equal to zero if $x$ is not an
integer.
Now let
\begin{equation}
r_{2s} (n) = \delta_{2s} (n) + e_{2s} (n).
\end{equation}
Then I can prove (see $\S$ 26) that
\begin{equation}
e_{2s} (n) = 0
\end{equation}
if $s = 1,2,3,4$ and that
\begin{equation}
e_{2s} (n) = O (n^{s-1-\frac{1}{2} [\frac{2}{3}s]+\epsilon)}
\end{equation}
for all positive integral values of $s$. But it is easy to see that, if $s
\geq 3,$ then
\begin{equation}
Hn^{s-1} \lt \delta_{2s} (n) \lt K n^{s-1},
\end{equation}
where $H$ and $K$ are positive constants. It follows that
\begin{equation}
r_{2s} (n) \sim \delta_{2s} (n)
\end{equation}
for all positive integral values of $s$.
It appears probable, from the empirical results I obtain at the end of this
paper, that
\begin{equation}
e_{2s} (n) = O \{n^{\frac{1}{2} (s-1) +\epsilon}\}
\end{equation}
for all positive integral values of $s$; and that
\begin{equation}
e_{2s} (n) \neq o \{n^{\frac{1}{2}(s-1)} \}
\end{equation}
if $s \geq 5$. But all that I can actually prove is that
\begin{equation}
e_{2s} (n) = O (n^{s-1-\frac{1}{2}[\frac{2}{3} s]})
\end{equation}
if $s \geq 9$ and that
\begin{equation}
e_{2s} (n) \neq o (n^{\frac{1}{2}s-1})
\end{equation}
if $s \geq 5$.
25. Let
\begin{equation}
f_{2s} (q) = \sum^\infty_1 e_{2s} (n) q^n = \sum^\infty_1 \{r_{2s}(n) -
\delta_{2s} (n) \} q^n.
\end{equation}
Then it can be shewn by the theory of elliptic functions that
\begin{equation}
f_{2s} (q) = \phi^{2s} (q) \sum_{1 \leq n \leq \myfrac{1}{4} (s-1)} K_n
(kk')^{2n},
\end{equation}
that is to say that
\begin{equation}
f_{2s} (q) = \frac{f^{4s}(-q)}{f^{2s}(q^2)} \sum_{1 \leq n \leq
\myfrac{1}{4} (s-1)} K_n \frac{f^{24n}(q^2)}{f^{24n}(-q)},
\end{equation}
where $\phi (q)$ and $f(q)$ are the same as in $\S$ 13. We thus obtain the
results contained in the following table.
TABLE VI
$$\begin{array}{lll}
1. & f_2 (q) = 0,\quad f_4 (q) = 0, \quad f_6(q) = 0,\quad f_8(q) =0. \\
2. & 5f_{10} (q) = 16 \frac{f^{14}(q^2)}{f^4(-q)}, \quad f_{12}(q) = 8
f^{12}(q^2). \\
3. & 61 f_{14}(q) = 728f^4 (-q) f^{10} (q^2), \quad 17 f_{16}(q)
= 256 f^8 (-q) f^8 (q^2). \\
4. & 1385 f_{18}(q) = 24416 f^{12} (-q) f^6 (q^2) - 256
\frac{f^{30}(q^2)}{f^{12}(-q)}. \\
5. & 31 f_{20} (q) = 616 f^{16} (-q) f^4 (q^2) - 128
\frac{f^{28}(q^2)}{f^8(-q)}.\\
6. & 50521 f_{22} (q) = 1103272 f^{20} (-q) f^2 (q^2) - 821888
\frac{f^{26}(q^2)}{f^4(-q)}.\\
7. & 691 f_{24} (q) = 16576 f^{24} (-q) - 32768 f^{24} (q^2).
\end{array}$$
It follows from the last formula of Table VI that
\begin{equation}
\myfrac{691}{64} e_{24} (n) = (-1)^{n-1} 259 \tau (n) - 512 \tau
(\half n),
\end{equation}
where $\tau (n)$ is the same as in $\S$ 16, and $\tau(x)$ should be considered
as equal to zero if $x$ is not an integer.
Results equivalent to 1,2,3,4 of Table VI were given by Dr. Glaisher in the
Quarterly Journal, Vol. XXXVIII. The arithmetical functions called by
him
$$ \chi_4 (n), \: \Omega(n), \: W(n), \: \Theta(n), \: U(n) $$
are the coefficients of $q^n$ in
$$\frac{f^{14}(q^2)}{f^4(-q)}, f^{12} (q^2), f^4(-q) f^{10}(q^2), f^8(q)
f^8(q^2), f^{12}(-q) f^6(q^2).$$
He gave reduction formulæ for these functions and observed how the
functions which I call $e_{10}(n), e_{12}(n)$ and $e_{16}(n)$ can be defined
by means of the complex divisors of $n$. It is very likely that $\tau(n)$
is also capable of such a definition.
26. Now let us consider the order of $e_{2s} (n)$. It is easy to see from
(147) that $f_{2s} (q)$ can be expressed in the form
\begin{equation}
\sum K_{a,b,c,h,k} \{ f^3(-q)\}^a
\left\{\frac{f^5(-q)}{f^2(q^2)}\right\}^b
\left\{\frac{f^5(q^2)}{f^2(-q)}\right\}^c f^h (-q) f^k(q^2),
\end{equation}
where $a, b, c, h, k$ are zero or positive integers, such that
$$a + b + c = [\myfrac{2}{3} s],\:\: h+k = 2s - 3 [\myfrac{2}{3}s].$$
Proceeding as in $\S$ 13 we can easily shew that
$$n^{-\frac{1}{2}[\frac{2}{3}s]} e_{2s} (n)$$
cannot be of higher order than the coefficient of $q^{24n}$ in
\begin{equation}
\phi^A (q) \phi^B (q^3) \phi^C (q^2),
\end{equation}
where $C$ is 0 or 1 and
$$ A + B + C = 2s - 2 [\myfrac{2}{3}s].$$
Now, if $s \geq 5, A + B + C \geq 4;$ and so $A + B \geq 3$. Hence one at
least of $A$ and $B$ is greater than 1. But we know that
$$ \phi^2 (q) = \sum O (\nu^\epsilon) q^\nu.$$
It follows that the coefficient of $q^{24n}$ in (150) is of order not
exceeding
$$n^{\frac{1}{2}(A + B + C)- 1+\epsilon}.$$
Thus
\begin{equation}
e_{2s} (n) = O(n^{s-1-\frac{1}{2} [\frac{2}{3}s]+ \epsilon})
\end{equation}
for all positive integral values of $s$.
27. When $ s \geq 9$ we can obtain a slightly more precise result.
If $s \geq 16$ we have $A + B + C \geq 12$; and so $A + B \geq 11$. Hence
one at least of $A$ and $B$ is greater than 5. But
$$ \phi^6 (q) = \sum O (\nu^2) q^\nu.$$
It follows that the coefficient of $q^{24n}$ in (150) is of order not
exceeding
$$ n^{\frac{1}{2}(A+B+C) -1},$$
or that
\begin{equation}
e_{2s} (n) = O (n^{s-1-\frac{1}{2}[\frac{2}{3}s]}),
\end{equation}
if $s \geq 16$. We can easily shew that
(152) is true when $9 \leq s \leq 16$
considering all the cases separately, using the identities.
\begin{eqnarray*}
&& f^{12} (-q) f^6 (q^2) = \{f^3 (-q)\}^4 ,
\{f^3(q^2)\}^2, \\
&&\frac{f^{30}(q^2)}{f^{12}(-q)} = \left\{\frac{f^5(q^2)}{f^2(-q)}\right\}^6,
\\
&&f^{16}(-q) f^4(q^2) = \left\{\frac{f^5(-q)}{f^2(q^2)}\right\}^4
\left\{\frac{f^5(q^2)}{f^2(-q)}\right\}^2 f^2(q^2), \\
&&\frac{f^{28}(q^2)}{f^8(-q)} = \left\{\frac{f^5(q^2)}{f^2(-q)}\right\}^4
\{f^3(q^2)\}^2 f^2(q^2), \cdots,
\end{eqnarray*}
and proceeding as in the previous two sections.
The argument of $\S\S$ 14-15 may also be applied to the function $e_{2s}
(n)$. We find that
\begin{equation}
e_{2s}(n) \neq o (n^{\frac{1}{2} s-1}).
\end{equation}
I leave the proof to the reader.
28. There is reason to suppose that
\begin{eqnarray}
\left. \begin{array}{ll}e_{2s} (n) = O \{n^{\frac{1}{2}
(s-1+\epsilon)}\}\\
e_{2s}(n) \neq o \{n^{\frac{1}{2}(s-1)}\} \end{array}\right\},
\end{eqnarray}
if $s\geq5$. I find, for example, that
\begin{equation}
\sum^\infty_1 \frac{e_{10}(n)}{n^s} = \frac{e_{10}(1)}{1+2^{2-s}} \Pi_1
\Pi_2,
\end{equation}
where
$$ \Pi_1 = \frac{1}{(1-3^{4-2s})(1-7^{4-2s})(1-11^{4-2s})\cdots},$$
3, 7, 11, $\ldots$ being the primes of the form $4n-1$, and
$$\Pi_2 = \frac{1}{(1-2c_5 \cdot 5^{-s} + 5^{4-2s}) (1-2c_{13} \cdot 13^{-s} +
13^{4-2s})\cdots}, $$
5, 13, 17, $\ldots$ being the primes of the form $4n+1$, and
$$c_p = u^2 - (4v)^2, $$
where $u$ and $v$ are the unique pair of positive integers satisfying the
equation
$$u^2 + (4v)^2 = p^2.$$
The equation
(155) is equivalent to the assertion that, if
$$n = (3^{a_3} \cdot 7^{a_7} \cdot 11^{a_{11}} \cdots)^2 \cdot 2^{a_2} \cdot
5^{a_5} \cdot 13^{a_{13}} \cdots, $$
where $a_p$ is zero or a positive integer, then
\begin{equation}
\frac{e_{10}(n)}{n^2 e_{10} (1)} = (-1)^{a_2} \frac{\sin 4
(1+a_5)\theta_5}{\sin 4 \theta_5} \cdot \frac{\sin 4
(1+a_{13})\theta_{13}}{\sin 4 \theta_{13}} \cdots,
\end{equation}
where
$$\tan \theta_p = \frac{u}{v} \:\:\:(0 \lt \theta_p \lt \half \pi),$$
$u$ and $v$ being integers satisfying the equation $u^2 + v^2 = p$; and
$e_{10}(n)=0$ otherwise. If this is true then we should have
\begin{equation}
\left| \frac{e_{10}(n)}{e_{10}(1)}\right| \leq n^2 d (n)
\end{equation}
for all values of $n$, and
\begin{equation}
\left| \frac{e_{10}(n)}{e_{10}(1)}\right| \geq n^2
\end{equation}
for an infinity of values of $n$. In this case we can prove that, if $n$ is
the square of a prime of the form $4m-1$, then
$$\left| \frac{e_{10}(n)}{e_{10}(1)}\right| = n^2. $$
Similarly I find that
\begin{equation}
\sum^\infty_1 \frac{e_{12}(n)}{n^s} = e_{12} (1) \prod_p
\left(\frac{1}{1+2c_p \cdot p^{-s} + p^{5-2s}}\right),
\end{equation}
$p$ being an odd prime and $c_p^2 \leq p^5$. From this it would follow that
\begin{equation}
\left| \frac{e_{12}(n)}{e_{12}(1)}\right| \leq n^{\frac{5}{2}} d (n)
\end{equation}
for all values of $n$, and
\begin{equation}
\left| \frac{e_{12}(n)}{e_{12}(1)}\right| \geq n^{\frac{5}{2}}
\end{equation}
for an infinity of values of $n$.
Finally I find that
\begin{equation}
\sum^\infty_1\frac{e_{16}(n)}{n^s}= \frac{e_{16}(1)}{1+2^{3-s}}
\prod_p \left(\frac{1}{1+2c_p \cdot p^{-s} + p^{7-2s}}\right),
\end{equation}
$p$ being an odd prime and $c_p^2 \leq p^7$. From this it would follow that
\begin{equation}
\left| \frac{e_{16}(n)}{e_{16}(1)}\right| \leq n^{\frac{7}{2}} d (n)
\end{equation}
for all values of $n$, and
\begin{equation}
\left| \frac{e_{16}(n)}{e_{16}(1)}\right| \geq n^{\frac{7}{2}}
\end{equation}
for an infinity of values of $n$.
In the case in which $2s = 24$ we have
$$ \myfrac{691}{64} e_{24} (n) = (-1)^{n-1} 259 \tau (n) - 512 \tau (\half
n).$$
I have already stated the reasons for supposing that
$$|\tau (n) | \leq n^{\frac{11}{2}} d(n) $$
for all values of $n$, and
$$ | \tau (n)| \geq n^{\frac{11}{2}} $$
for an infinity of values of $n$.
1Knopp, Dissertation (Berlin, 1907), p.34.
2(10) follows from this as an immediate corollary.
3For example when $r=1$ and $s=9$ this inequality becomes $1.64493\ldots \lt 1.64616\ldots \lt 1.64697\ldots \lt 1.64823\ldots$.
4If $x = q^2$, then in the notation of elliptic functions
\begin{eqnarray*}
P&=& \frac{12 \eta \omega}{\pi^2} = \left(\frac{2K}{\pi}\right)^2 \left(
\frac{3E}{K} + k^2 - 2 \right), \\
Q &=& \frac{12 g_2 \omega^4}{\pi^4} = \left(\frac{2K}{\pi}\right)^4 (1-k^2 +
k^4), \\
R &=& \frac{216 g_3 \omega^6}{\pi^6} = \left(\frac{2K}{\pi}\right)^6
(1+k^2)(1-2k^2) (1- \half k^2).
\end{eqnarray*}
5See $\S\S$24--25.
6Acta Mathematica, Vol.XXXVII, pp. 193 -- 238.
7$\Psi_6 (n)$ is Dr. Glaisher's $\lambda (n)$.
