Let $PQR$ be a circle with center $O$, of which a diameter is $PR$. Bisect $PO$ at $H$ and let $T$ be the point of trisection of $OR$ nearer $R$. Draw $TQ$ perpendicular to $PR$ and place the chord $RS=TQ$.
Join $PS$, and draw $OM$ and $TN$ parallel to $RS$. Place a chord $PK=PM,$ and draw the tangent $PL=MN$. Join $RL, RK$ and $KL$. Cut off $RC=RH$. Draw $CD$ parallel to $KL,$ meeting $RL$ at $D$.
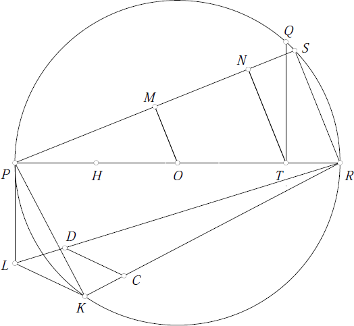
Then the square on $RD$ will be equal to the circle $PQR$ approximately. For $$ RS^2 = \frac{5}{36} d^2,$$ where $d$ is the diameter of the circle. Therefore $$PS^2 = \frac{31}{36} d^2.$$ But $PL$ and $PK$ are equal to $MN$ and $PM$ respectively. Therefore $$PK^2 = \frac{31}{144} d^2, \mbox{and } PL^2 = \frac{31}{324} d^2.$$ Hence $$ RK^2 = PR^2 - PK^2 = \frac{113}{144} d^2 , $$ and $$ RL^2 = PR^2 + PL^2 = \frac{355}{324} d^2. $$
But $$ \frac{RK}{RL} = \frac{RC}{RD} = \frac{3}{2} \sqrt{\frac{113}{355}},$$ and $$ RC = \frac{3}{4} d.$$ Therefore $$RD =\frac{d}{2} \sqrt{\frac{355}{113}} = r\sqrt{\pi}, \mbox{very nearly } $$
Note: If the area of the circle be 140,000 square miles, then $RD$ is greater than the true length by about an inch.