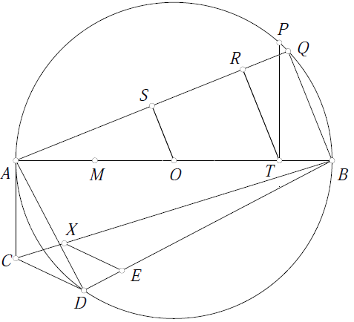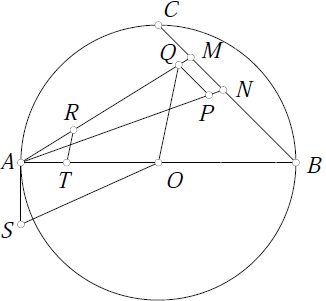1. If we suppose that

and then $G_n$ and $g_n$ can always be expressed as roots of algebraical equations when $n$ is any rational number. For we know that and

Now the relation between the moduli $k$ and $l$, which makes $$ n \frac{K'}{K} = \frac{L'}{L}, $$ where $n = r/s, r$ and $s$ being positive integers, is expressed by the modular equation of the $rs$th degree. If we suppose that $k=l', k'=l,$ so that $K = L', K'=L$, then $$ q = e^{-\pi L'/L} = e^{-\pi \sqrt{n}},$$ and the corresponding value of $k$ may be found by the solution of an algebraical equation. From (1), (2), (3) and (4) it may easily be deduced that

I shall consider only integral values of $n$. It follows from (7) that we need consider only one of $G_n$ or $g_n$ for any given value of $n$; and from (5) that we may suppose $n$ not divisible by 4. It is most convenient to consider $g_n$ when $n$ is even, and $G_n$ when $n$ is odd.

2. Suppose then that $n$ is odd. The values of $G_n$ and $g_{2n}$ are got from the same modular equation. For example, let us take the modular equation of the 5th degree, viz.

where $$ 2^{\frac{1}{4}} q^{\frac{1}{24}} u = (1+q) (1+q^3) (1+q^5)\cdots$$ and $$ 2^{\frac{1}{4}} q^{\frac{5}{24}} v = (1+q^5) (1+q^{15})(1+q^{25})\cdots $$ By changing $q$ to $-q$ the above equation may also be written as where $$2^{\frac{1}{4}} q^{\frac{1}{24}} u = (1-q) (1-q^3) (1-q^5)\cdots$$ and $$ 2^{\frac{1}{4}} q^{\frac{5}{24}} v = (1-q^5) (1-q^{15}) (1-q^{25})\cdots$$ If we put $q = e^{-\pi/\sqrt{5}}$ in (8), so that $u = G_{\frac{1}{5}}$ and $v=G_5$, and hence $u=v$, we see that $$v^4 -v^{-4} = 1.$$ Hence $$ v^4 = \frac{1 +\sqrt{5}}{2}, G_5 = \left(\frac{1+\sqrt{5}}{2}\right)^{\frac{1}{4}}.$$ Similarly, by putting $q=e^{- \pi \sqrt{\frac{2}{5}}},$ so that $u = g_{\frac{2}{5}}$ and $ v=g_{10}$, and hence $u=1/v$, we see that $$v^6 - v^{-6} = 4.$$ Hence $$ v^2 = \frac{1+\sqrt{5}}{2}, g_{10} = \sqrt{\frac{1+\sqrt{5}}{2}}.$$ Similarly it can be shewn that \begin{eqnarray*} G_9 &=& \left(\frac{1+\sqrt{3}}{\sqrt{2}}\right)^{\frac{1}{3}}, \quad g_{18}= (\sqrt{2}+\sqrt{3})^{\frac{1}{3}}, \\ G_{17} &=& \sqrt{\left(\frac{5 + \sqrt{17}}{8}\right)} + \sqrt{\left(\frac{\sqrt{17}-3}{8}\right)}, \\ g_{34} &=& \sqrt{\left(\frac{7+\sqrt{17}}{8}\right)} + \sqrt{\left(\frac{\sqrt{17}-1}{8}\right)}, \end{eqnarray*} and so on.

3. In order to obtain approximations for $\pi$ we take logarithms of (1) and (2). Thus

approximately, the error being nearly $\frac{24}{\sqrt{n}} e^{-\pi \sqrt{n}}$ in both cases. These equations may also be written as In those cases in which $G_n^{12}$ and $g_n^{12}$ are simple quadratic surds we may use the forms $$(G_n^{12} + G_n^{-12})^{\frac{1}{12}}, (g_n^{12} + g_n^{-12})^{\frac{1}{12}},$$ instead of $G_n$ and $g_n$, for we have $$g_n^{12} = \frac{1}{8} e^{\frac{1}{2} \pi \sqrt{n}} - \frac{3}{2} e^{-\frac{1}{2} \pi \sqrt{n}}, $$ approximately, and so $$g_n^{12} + g_n^{-12} = \frac{1}{8} e^{\frac{1}{2} \pi \sqrt{n}} + \frac{13}{2} e^{-\frac{1}{2} \pi \sqrt{n}},$$ approximately, so that the error being about $\frac{104}{\sqrt{n}} e^{-\pi \sqrt{n}}$, which is of the same order as the error in the formulæ (10). The formula (12) often leads to simpler results. Thus the second of formulæ (10) gives $$e^{\pi \sqrt{18}/24} = 2^{\frac{1}{4}} g_{18} $$ or $$e^{\frac{1}{4} \pi \sqrt{18}} = 10 \sqrt{2} + 8 \sqrt{3}.$$ But if we use the formula (12), or $$e^{\pi \sqrt{n}/24} = 2^{\frac{1}{4}} (g_n^{12} + g_n^{-12})^{\frac{1}{12}},$$ we get a simpler form, viz. $$e^{\frac{1}{8} \pi \sqrt{18}} = 2 \sqrt{7}.$$

4. The values of $g_{2n}$ and $G_n$ are obtained from the same equation. The approximation by means of $g_{2n}$ is preferable to that by $G_n$ for the following reasons.

(a) It is more accurate. Thus the error when we use $G_{65}$ contains a factor $e^{- \pi \sqrt{65}}$, whereas that when we use $g_{130}$ contains a factor $e^{-\pi \sqrt{130}}$.

(b) For many values of $n$, $g_{2n}$ is simpler in form than $G_n$; thus $$g_{130} = \sqrt{ \left\{ (2 + \sqrt{5}) \left(\frac{3 + \sqrt{13}}{2}\right)\right\}}, $$ while $$G_{65}= \left\{\left(\frac{1+\sqrt{5}}{2}\right) \left(\frac{3+\sqrt{13}}{2}\right)\right\}^{\frac{1}{4}} \sqrt{\left\{\sqrt{\left(\frac{9+\sqrt{65}}{8}\right)} + \sqrt{\left(\frac{1+\sqrt{65}}{8}\right)}\right\}}.$$

(c) For many values of $n$, $g_{2n}$ involves quadratic surds only, even when $G_n$ is a root of an equation of higher order. Thus $G_{23}, G_{29}, G_{31}$ are roots of cubic equations, $G_{47}, G_{79}$ are those of quintic equations, and $G_{71}$ is that of a septic equation, while $g_{46}, g_{58}, g_{62}, g_{94}, g_{142}$ and $g_{158}$ are all expressible by quadratic surds.

5. Since $G_n$ and $g_n$ can be expressed as roots of algebraical equations with rational coefficients, the same is true of $G_n^{24}$ or $g_n^{24}$. So let us suppose that $$ 1 = ag_n^{-24} - bg_n^{-48} + \cdots,$$ or $$g_n^{24} = a- bg_n^{-24} + \cdots .$$ But we know that \begin{eqnarray*} 64 e^{-\pi \sqrt{n}} g_n^{24} = 1 - 24 e^{-\pi \sqrt{n}} + 276 e^{-2\pi \sqrt{n}} - \cdots, \\ 64 g_n^{24} = e^{\pi \sqrt{n}} - 24 + 276 e^{-\pi \sqrt{n}} - \cdots,\\ 64a - 64 bg_n^{-24} + \cdots = e^{\pi \sqrt{n}} - 24 + 276 e^{-\pi \sqrt{n}} - \cdots,\\ 64 a - 4096be^{-\pi \sqrt{n}} + \cdots = e^{\pi \sqrt{n}} - 24 + 276 e^{-\pi \sqrt{n}} - \cdots, \end{eqnarray*} that is

Similarly, if $$1= a G_n^{-24} - b G_n^{-48} + \cdots, $$ then

From (13) and (14) we can find whether $e^{\pi \sqrt{n}}$ is very nearly an integer for given values of $n$, and ascertain also the number of 9's or 0's in the decimal part. But if $G_n$ and $g_n$ be simple quadratic surds we may work independently as follows. We have, for example, $$g_{22} = \sqrt{(1+ \sqrt{2})}.$$ Hence \begin{eqnarray*} 64 g_{22}^{24} &=& e^{\pi \sqrt{22}} - 24 + 276 e^{- \pi \sqrt{22}} - \cdots, \\ 64g_{22}^{-24}&=& \hphantom{e^{\pi \sqrt{22}} - 24 +} 4096 e^{-\pi \sqrt{22}} + \cdots, \end{eqnarray*} so that $$ 64(g_{22}^{24} + g_{22}^{-24}) = e^{\pi \sqrt{22}} - 24 + 4372 e^{-\pi \sqrt{22}} + \cdots = 64 \{(1+\sqrt{2})^{12} + (1- \sqrt{2})^{12}\}.$$ Hence $$e^{\pi \sqrt{22}} = 2508951.9982\ldots.$$ Again $$ G_{37} = (6 + \sqrt{37})^{\frac{1}{4}},$$ \begin{eqnarray*} 64 G_{37}^{24} &=& e^{\pi \sqrt{37}} + 24 + 276 e^{-\pi \sqrt{37}} + \cdots ,\\ 64 G_{37}^{-24} &=& \hphantom{e^{\pi \sqrt{37}} + 24 +} 4096 e^{-\pi \sqrt{37}} - \cdots, \end{eqnarray*} so that $$ 64 (G_{37}^{24} + G_{37}^{-24}) = e^{\pi \sqrt{37}} + 24 + 4372 e^{-\pi \sqrt{37}} - \cdots = 64 \{(6 + \sqrt{37})^6 + (6- \sqrt{37})^6 \}.$$ Hence $$ e^{\pi \sqrt{37}} = 199148647.999978 \ldots.$$ Similarly, from $$ g_{58} = \sqrt{\left(\frac{5 + \sqrt{29}}{2}\right)},$$ we obtain $$64(g_{58}^{24} + g_{58}^{-24}) = e^{\pi \sqrt{58}} - 24 + 4372 e^{-\pi \sqrt{58}} + \cdots = 64 \left\{\left(\frac{5 + \sqrt{29}}{2}\right)^{12} + \left(\frac{5-\sqrt{29}}{2}\right)^{12}\right\}.$$ Hence $$e^{\pi \sqrt{58}} = 24591257751.99999982\ldots.$$

6. I have calculated the values of $G_n$ and $g_n$ for a large number of values of $n$. Many of these results are equivalent to results given by Weber; for example, \begin{eqnarray*} G_{13}^4 &=& \frac{3+\sqrt{13}}{2}, G_{25} = \frac{1+\sqrt{5}}{2},\\[2mm] g_{30}^6 &=& (2+ \sqrt{5}) (3 + \sqrt{10}), G_{37}^4 = 6 + \sqrt{37},\\[2mm] G_{49} &=& \frac{7^{\frac{1}{4}} + \sqrt{(4 + \sqrt{7})}}{2}, g_{58}^2 = \frac{5+\sqrt{29}}{2},\\[2mm] g_{70}^2 &=& \frac{(3+\sqrt{5}) (1+ \sqrt{2})}{2},\\[2mm] G_{73} &=& \sqrt{\left(\frac{9 + \sqrt{73}}{8}\right)} + \sqrt{\left(\frac{1+\sqrt{73}}{8}\right)},\\[2mm] G_{85} &=& \left(\frac{1+\sqrt{5}}{2}\right) \left(\frac{9+\sqrt{85}}{2}\right)^{\frac{1}{4}}, \\[2mm] G_{97} &=& \sqrt{\left(\frac{13+\sqrt{97}}{8}\right)} + \sqrt{\left(\frac{5 + \sqrt{97}}{8}\right)},\\[2mm] g_{190}^2 &=& (2 + \sqrt{5}) (3 + \sqrt{10}), \\[2mm] G_{385}^2 &=& \frac{1}{8} (3 + \sqrt{11}) (\sqrt{5} + \sqrt{7}) (\sqrt{7}+\sqrt{11}) (3 + \sqrt{5}), \end{eqnarray*} and so on. I have also many results not given by Weber. I give a complete table of new results. In Weber's notation, $G_n = 2^{-\frac{1}{4}} f \{\sqrt{(-n)}\}$ and $g_n = 2^{-\frac{1}{4}} f_1 \{\sqrt{(-n)}\}.$

\begin{eqnarray*} g_{62} &+& \frac{1}{g_{62}} = \frac{1}{2} \{ \sqrt{(1+\sqrt{2})} + \sqrt{(9+5 \sqrt{2})} \},\\[2mm] G_{65}^2 &=& \sqrt{\left\{\left(\frac{1+\sqrt{5}}{2}\right) \left(\frac{3+\sqrt{13}}{2}\right)\right\}} \left\{\sqrt{\left(\frac{1+\sqrt{65}}{8}\right)} + \sqrt{\left(\frac{9+\sqrt{65}}{8}\right)}\right\},\\[2mm] g_{66}^2 &=& \sqrt{(\sqrt{2} + \sqrt{3})} (7 \sqrt{2} + 3 \sqrt{11})^{\frac{1}{6}} \left\{\sqrt{\left(\frac{7 + \sqrt{33}}{8}\right)} + \sqrt{\left(\frac{\sqrt{33}-1}{8}\right)}\right\},\\[2mm] G_{69}^2 &=& (3\sqrt{3} + \sqrt{23})^{\frac{1}{4}} \left(\frac{5 + \sqrt{23}}{4}\right)^{\frac{1}{6}} \left\{ \sqrt{\left( \frac{6+3 \sqrt{3}}{4}\right)} + \sqrt{\left(\frac{2 + 3\sqrt{3}}{4}\right)}\right\},\\[2mm] G_{77}^2 &=& \{\frac{1}{2} (\sqrt{7} + \sqrt{11}) (8 + 3 \sqrt{7})\}^{\frac{1}{4}} \left\{\sqrt{\left(\frac{6 + \sqrt{11}}{4}\right)} + \sqrt{\left(\frac{2 + \sqrt{11}}{4}\right)}\right\},\\[2mm] G_{81}^3 &=& \frac{(2 \sqrt{3} + 2)^{\frac{1}{3}} + 1}{(2 \sqrt{3} - 2)^{\frac{1}{3}}-1},\\[2mm] g_{90} &=& \{(2 + \sqrt{5}) (\sqrt{5} + \sqrt{6})\}^{\frac{1}{6}} \left\{\sqrt{\left(\frac{3 + \sqrt{6}}{4}\right)} + \sqrt{\left(\frac{\sqrt{6}-1}{4}\right)}\right\},\\[2mm] g_{94} &+& \frac{1}{g_{94}} = \frac{1}{2} \{\sqrt{(7 + \sqrt{2})} + \sqrt{(7 + 5 \sqrt{2})}\},\\[2mm] g_{98} &+& \frac{1}{g_{98}} = \frac{1}{2} \{\sqrt{2} + \sqrt{(14 + 4 \sqrt{14})}\},\\[2mm] g_{114}^2 &=& \sqrt{(\sqrt{2} + \sqrt{3})} (3 \sqrt{2} + \sqrt{19})^{\frac{1}{6}} \left\{\sqrt{\left(\frac{23+3 \sqrt{57}}{8}\right)} + \sqrt{\left(\frac{15 + 3 \sqrt{57}}{8}\right)}\right\},\\[2mm] G_{117} &=& \frac{1}{2} \left(\frac{3 + \sqrt{13}}{2}\right)^{\frac{1}{4}} (2 \sqrt{3} + \sqrt{13})^{\frac{1}{6}} \{3^{\frac{1}{4}} + \sqrt{(4 + \sqrt{3})}\}, \end{eqnarray*} \begin{eqnarray*} \left.\begin{array}{lll} G_{121} &+& \ds{\frac{1}{G_{121}}} = \left(\frac{11}{2}\right)^{\frac{1}{6}} \left\{\left(3 + \frac{1}{3\sqrt{3}}\right)^{\frac{1}{3}} + \left(3-\frac{1}{3 \sqrt{3}}\right)^{\frac{1}{3}} \right\}\\[3mm] \ds{\frac{1}{G_{121}}} &=& \frac{1}{3\sqrt{2}} [(11- 3 \sqrt{11})^{\frac{1}{3}} \{(3 \sqrt{11} + 3 \sqrt{3} - 4)^{\frac{1}{3}} + (3 \sqrt{11} - 3 \sqrt{3} - 4)^{\frac{1}{3}} \} - 2] \end{array}\right\}, \end{eqnarray*} \begin{eqnarray*} g_{126} &=& \sqrt{\left(\frac{\sqrt{3} + \sqrt{7}}{2}\right)} (\sqrt{6} + \sqrt{7})^{\frac{1}{6}} \left\{\sqrt{\left(\frac{3 + \sqrt{2}}{4}\right)} + \sqrt{\left(\frac{\sqrt{2} - 1}{4}\right)}\right\}^2,\\[2mm] g_{138}^2 &=& \sqrt{\left(\frac{3 \sqrt{3} + \sqrt{23}}{2}\right)} (78 \sqrt{2} + 23 \sqrt{23})^{\frac{1}{6}} \times \left\{\sqrt{\left(\frac{5+2\sqrt{6}}{4}\right)} + \sqrt{\left(\frac{1+2 \sqrt{6}}{4}\right)}\right\},\\[2mm] G_{141}^2 &=& (4 \sqrt{3} + \sqrt{47})^{\frac{1}{4}} \left(\frac{7 + \sqrt{47}}{\sqrt{2}}\right)^{\frac{1}{6}} \left\{\sqrt{\left(\frac{18 + 9 \sqrt{3}}{4}\right)} + \sqrt{\left(\frac{14+9\sqrt{3}}{4}\right)}\right\},\\[2mm] G_{145}^2 &=& \sqrt{\left\{\frac{(2 + \sqrt{5})(5+\sqrt{29})}{2}\right\}} \left\{\sqrt{\left(\frac{17+\sqrt{145}}{8}\right)} + \sqrt{\left(\frac{9 + \sqrt{145}}{8}\right)}\right\},\\[2mm] \frac{1}{G_{147}} &=& 2^{-\frac{1}{12}} \left[\frac{1}{2} +\frac{1}{\sqrt{3}} \left\{\sqrt{\left(\frac{7}{4}\right) - (28)^{\frac{1}{6}}}\right\}\right], \\[2mm] G_{153} &=& \left\{\sqrt{\left(\frac{5 + \sqrt{17}}{8}\right)} + \sqrt{\left(\frac{\sqrt{17}-3}{8}\right)}\right\}^2\\[2mm] && \times \left\{\sqrt{\left(\frac{37+9\sqrt{17}}{4}\right)} +\sqrt{\left(\frac{33+9\sqrt{17}}{4}\right)}\right\}^{\frac{1}{3}},\\[2mm] g_{154}^2 &=& \sqrt{\left\{(2 \sqrt{2} + \sqrt{7}) \left(\frac{\sqrt{7}+\sqrt{11}}{2}\right)\right\}}\\[2mm] && \times \left\{\sqrt{\left(\frac{13+2\sqrt{22}}{4}\right)} +\sqrt{\left(\frac{9 + 2\sqrt{22}}{4}\right)}\right\},\\[2mm] g_{158} &+& \frac{1}{g_{158}} = \frac{1}{2} \{\sqrt{(9 + \sqrt{2})} + \sqrt{(17 +13 \sqrt{2})}\}, \end{eqnarray*} \begin{eqnarray*}\left.\begin{array}{lll} G_{169} &+& \ds{\frac{1}{G_{169}}} = \ds\left(\frac{13}{4}\right)^{\frac{1}{6}} \left\{\left(1 + \frac{1}{3\sqrt{3}}\right)^{\frac{1}{3}} + \left(1 - \frac{1}{3 \sqrt{3}}\right)^{\frac{1}{3}}\right\}^2 \\[2mm] \ds{\frac{1}{G_{169}}} &=& \ds\frac{1}{3} \left[(\sqrt{13} - 2) + \left(\frac{13-3 \sqrt{13}}{2}\right)^{\frac{1}{3}}\right. \\[2mm] && \ds\left.\times \left\{\left(3 \sqrt{3} - \frac{11 - \sqrt{13}}{2}\right)^{\frac{1}{3}} - \left(3 \sqrt{3} + \frac{11-\sqrt{13}}{2}\right)^{\frac{1}{3}}\right\} \right] \end{array}\right\}, \end{eqnarray*}

\begin{eqnarray*} g_{198} &=& \sqrt{(1+\sqrt{2})} (4 \sqrt{2} + \sqrt{33})^{\frac{1}{6}} \left\{\sqrt{\left(\frac{9+\sqrt{33}}{8}\right)} +\sqrt{\left(\frac{1+\sqrt{33}}{8}\right)}\right\},\\[2mm] G_{205} &=& \left(\frac{1+\sqrt{5}}{2}\right) \left(\frac{3\sqrt{5} +\sqrt{41}}{2}\right)^{\frac{1}{4}} \left\{\sqrt{\left(\frac{7+\sqrt{41}}{8}\right)} +\sqrt{\left(\frac{\sqrt{41}-1}{8}\right)}\right\},\\[2mm] G_{213}^2 &=& ( 5 \sqrt{3} + \sqrt{71})^{\frac{1}{4}} \left(\frac{59+7\sqrt{71}}{4}\right)^{\frac{1}{6}}\\[2mm] && \times \left\{\sqrt{\left(\frac{21+12\sqrt{3}}{2}\right)} + \sqrt{\left(\frac{19+12\sqrt{3}}{2}\right)}\right\},\\[2mm] G_{217}^2 &=& \left\{\sqrt{\left(\frac{9+4\sqrt{7}}{2}\right)} +\sqrt{\left(\frac{11 + 4\sqrt{7}}{2}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{12+5\sqrt{7}}{4}\right)} + \sqrt{\left(\frac{16 + 5\sqrt{7}}{4}\right)}\right\},\\[2mm] G_{225}&=& \left(\frac{1 + \sqrt{5}}{4}\right) (2 + \sqrt{3})^{\frac{1}{3}} \{\sqrt{(4 + \sqrt{15})} + 15^{\frac{1}{4}}\},\\[2mm] g_{238} &=& \left\{\sqrt{\left(\frac{1+2\sqrt{2}}{4}\right)} +\sqrt{\left(\frac{5+2\sqrt{2}}{4}\right)}\right\}\\[2mm] &&\times \left\{\sqrt{\left(\frac{1+3\sqrt{2}}{4}\right)} +\sqrt{\left(\frac{5+3\sqrt{2}}{4}\right)}\right\},\\[2mm] G_{265}^2 &=& \sqrt{\left\{(2 + \sqrt{5}) \left(\frac{7+\sqrt{53}}{2}\right)\right\}} \left\{\sqrt{\left(\frac{89+5\sqrt{265}}{8}\right)} + \sqrt{\left(\frac{81+5\sqrt{265}}{8}\right)}\right\},\\[2mm] G_{289} &=& \left[\sqrt{\left\{\frac{17 + \sqrt{17} + 17^{\frac{1}{4}} (5+ \sqrt{17})}{16}\right\}} + \sqrt{\left\{\frac{1+\sqrt{17} +17^{\frac{1}{4}} (5 + \sqrt{17})}{16}\right\}}\right]^2,\\[2mm] G_{301}^2 &=& \left\{(8 + 3 \sqrt{7}) \left(\frac{23 \sqrt{43} + 57 \sqrt{7}}{2}\right)\right\}^{\frac{1}{4}} \\[2mm] && \times \left\{\sqrt{\left(\frac{46 + 7 \sqrt{43}}{4}\right)} + \sqrt{\left(\frac{42+ 7 \sqrt{43}}{4}\right)}\right\},\\[2mm] g_{310} &=& \left(\frac{1+\sqrt{5}}{2}\right) \sqrt{(1+\sqrt{2})} \left\{\sqrt{\left(\frac{7 + 2\sqrt{10}}{4}\right)} + \sqrt{\left(\frac{3 + 2 \sqrt{10}}{4}\right)}\right\},\\[2mm] \end{eqnarray*}

\begin{eqnarray*} \left.\begin{array}{lll} G_{325} &=& \ds\left(\frac{3+\sqrt{13}}{2}\right)^{\frac{1}{4}} t, \mbox{where } \\[2mm] &&\ds t^3 + t^2 \left(\frac{1-\sqrt{13}}{2}\right)^2 + t\left(\frac{1+\sqrt{13}}{2}\right)^2 + 1\\[2mm] &&= \sqrt{5} \left\{t^3 - t^2 \left(\frac{1+\sqrt{13}}{2}\right) + t\left(\frac{1-\sqrt{13}}{2}\right)-1\right\}\end{array}\right\}, \end{eqnarray*} \begin{eqnarray*} G_{333} &=& \frac{1}{2} (6+ \sqrt{37})^{\frac{1}{4}} (7\sqrt{3} + 2 \sqrt{37})^{\frac{1}{6}} \{\sqrt{(7 +2 \sqrt{3})} + \sqrt{(3+2 \sqrt{3})}\}, \end{eqnarray*} \begin{eqnarray*}\left.\begin{array}{lll} G_{363} &=& 2^{\frac{5}{12}} t, \mbox{where }\\[2mm] && 2t^3 - t^2 \{(4 + \sqrt{33}) + \sqrt{(11 + 2 \sqrt{33})}\}\\[2mm] &&-t\{1+\sqrt{(11 + 2\sqrt{33})}\}-1 = 0 \end{array}\right\}, \end{eqnarray*} \begin{eqnarray*} G_{441}^2 &=& \left(\frac{\sqrt{3}+\sqrt{7}}{2}\right) (2+\sqrt{3})^{\frac{1}{3}} \left\{\frac{2 + \sqrt{7} + \sqrt{(7+4 \sqrt{7})}}{2}\right\} \left\{\frac{\sqrt{(3+\sqrt{7})}+(6\sqrt{7})^{\frac{1}{4}}} {\sqrt{(3+\sqrt{7})}-(6\sqrt{7})^{\frac{1}{4}}}\right\},\\[2mm] G_{445}&=& \sqrt{(2 +\sqrt{5})} \left(\frac{21+\sqrt{445}}{2}\right)^{\frac{1}{4}} \sqrt{\left\{\left(\frac{13 +\sqrt{89}}{8}\right) + \sqrt{\left(\frac{5+\sqrt{89}}{8}\right)}\right\}},\\[2mm] G_{465}^2 &=& \sqrt{\left\{(2+\sqrt{3}) \left(\frac{1+\sqrt{5}}{2}\right) \left(\frac{3\sqrt{3} + \sqrt{31}}{2}\right)\right\}} (5\sqrt{5} + 2 \sqrt{31})^{\frac{1}{6}}\\[1mm] &&\times \left\{\sqrt{\left(\frac{2 + \sqrt{31}}{4}\right)} + \sqrt{\left(\frac{6 + \sqrt{31}}{4}\right)}\right\}\\[1mm] && \times \left\{\sqrt{\left(\frac{11+2\sqrt{31}}{2}\right)} + \sqrt{\left(\frac{13+2\sqrt{31}}{2}\right)}\right\},\\[2mm] G_{505}^2 &=& (2 + \sqrt{5}) \sqrt{\left\{\left(\frac{1+\sqrt{5}}{2}\right) (10 + \sqrt{101})\right\}}\\[2mm] && \times \left\{\left(\frac{5\sqrt{5} + \sqrt{101}}{4}\right) + \sqrt{\left(\frac{105 + \sqrt{505}}{8}\right)} \right\},\\[2mm] g_{522} &=& \sqrt{\left(\frac{5 + \sqrt{29}}{2}\right)} (5 \sqrt{29} + 11 \sqrt{6})^{\frac{1}{6}} \left\{\sqrt{\left(\frac{9+3\sqrt{6}}{4}\right)} + \sqrt{\left(\frac{5+3\sqrt{6}}{4}\right)}\right\},\\[2mm] G_{553}^2 &=& \left\{\sqrt{\left(\frac{96 + 11 \sqrt{79}}{4}\right)} + \sqrt{\left(\frac{100+11\sqrt{79}}{4}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{141+16\sqrt{79}}{2}\right)} + \sqrt{\left(\frac{143+16 \sqrt{79}}{2}\right)}\right\},\\[2mm] g_{630} &=& (\sqrt{14} + \sqrt{15})^{\frac{1}{6}} \sqrt{\left\{(1+\sqrt{2}) \left(\frac{3 + \sqrt{5}}{2}\right) \left(\frac{\sqrt{3} + \sqrt{7}}{2}\right)\right\}}\\[2mm] && \times \left\{\sqrt{\left(\frac{\sqrt{15} + \sqrt{7} + 2}{4}\right)} + \sqrt{\left(\frac{\sqrt{15} + \sqrt{7}-2}{4}\right)}\right\}\\[2mm] &&\times \left\{\sqrt{\left(\frac{\sqrt{15} + \sqrt{7} + 4}{8}\right)} + \sqrt{\left(\frac{\sqrt{15}+\sqrt{7}-4}{8}\right)}\right\},\\[2mm] G_{765}^2 &=& \left(\frac{3 + \sqrt{5}}{2}\right) (16 + \sqrt{255})^{\frac{1}{6}} \sqrt{\left\{ (4+ \sqrt{15}) \left(\frac{9+\sqrt{85}}{2}\right)\right\}}\\[2mm] && \times \left\{\sqrt{\left(\frac{6+\sqrt{51}}{4}\right)} + \sqrt{\left(\frac{10 + \sqrt{51}}{4}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{18+3\sqrt{51}}{4}\right)} + \sqrt{\left(\frac{22+3\sqrt{51}}{4}\right)}\right\},\\[2mm] G_{777}^2 &=& \sqrt{\left\{(2+\sqrt{3}) (6 + \sqrt{37}) \left(\frac{\sqrt{3}+\sqrt{7}}{2}\right)\right\}} (246 \sqrt{7} + 107 \sqrt{37})^{\frac{1}{6}}\\[2mm] && \times \left\{\sqrt{\left(\frac{6+3\sqrt{7}}{4}\right)} + \sqrt{\left(\frac{10+3\sqrt{7}}{4}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{15+6\sqrt{7}}{2}\right)} + \sqrt{\left(\frac{17+6\sqrt{7}}{2}\right)}\right\},\\[2mm] G_{1225} &=& \left(\frac{1+\sqrt{5}}{2}\right) (6+\sqrt{35})^{\frac{1}{4}} \left\{\frac{7^{\frac{1}{4}} + \sqrt{(4+\sqrt{7})}}{2}\right\}^{\frac{3}{2}}\\[2mm] && \times \left[\sqrt{\left\{\frac{43+15\sqrt{7} + (8 + 3\sqrt{7}) \sqrt{(10 \sqrt{7})}}{8} \right\}}\right.\\[2mm] && \left.+ \sqrt{\left\{\frac{35 + 15\sqrt{7} + (8 + 3\sqrt{7}) \sqrt{(10 \sqrt{7})}}{8}\right\}}~\right],\\[2mm] G_{1353}^2 &=& \sqrt{\left\{(3+\sqrt{11}) (5+3\sqrt{3}) \left(\frac{11+\sqrt{123}}{2}\right)\right\}}\\[2mm] && \times \left(\frac{6817 + 321 \sqrt{451}}{4}\right)^{\frac{1}{6}}\\[2mm] && \times \left\{\sqrt{\left(\frac{17+3\sqrt{33}}{8}\right)} + \sqrt{\left(\frac{25+3\sqrt{33}}{8}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{561+99\sqrt{33}}{8}\right)} +\sqrt{\left(\frac{569+99\sqrt{33}}{8}\right)}\right\},\\[2mm] G_{1645}^2 &=& (2+\sqrt{5}) \sqrt{\left\{(3+\sqrt{7}) \left(\frac{7+\sqrt{47}}{2}\right)\right\}} \left(\frac{73\sqrt{5} + 9\sqrt{329}}{2}\right)^{\frac{1}{4}}\\[2mm] && \times \left\{\sqrt{\left(\frac{119+7\sqrt{329}}{8}\right)} + \sqrt{\left(\frac{127+7\sqrt{329}}{8}\right)}\right\}\\[2mm] && \times \left\{\sqrt{\left(\frac{743+41\sqrt{329}}{8}\right)} + \sqrt{\left(\frac{751+41\sqrt{329}}{8}\right)}\right\}. \end{eqnarray*}

7. Hence we deduce the following approximate formulæ

\begin{eqnarray*} e^{\frac{1}{8}\pi \sqrt{18}} &=& 2 \sqrt{7}, e^{\pi \sqrt{22/12}} = 2 + \sqrt{2}, e^{\frac{1}{4}\pi \sqrt{30}} = 20 \sqrt{3} + 16 \sqrt{6},\\[2mm] e^{\frac{1}{4}\pi \sqrt{34}} &=& 12(4 +\sqrt{17}), e^{\frac{1}{2}\pi \sqrt{46}} = 144 (147 + 104 \sqrt{2})\\[2mm] e^{\frac{1}{4}\pi \sqrt{42}} &=& 84+32\sqrt{6}, e^{\pi \sqrt{58/12}} = \frac{5+\sqrt{29}}{\sqrt{2}}, \\[2mm] e^{\frac{1}{4} \pi \sqrt{70}} &=& 60 \sqrt{35} + 96 \sqrt{14}, e^{\frac{1}{4} \pi \sqrt{78}} = 300 \sqrt{3} + 208 \sqrt{6},\\[2mm] e^{\pi \sqrt{55/24}} &=& \frac{1+\sqrt{(3+2 \sqrt{5})}}{\sqrt{2}}, e^{\frac{1}{4}\pi \sqrt{102}} = 800 \sqrt{3} + 196 \sqrt{51},\\[2mm] e^{\frac{1}{4} \pi \sqrt{130}} &=& 12 (323 + 40 \sqrt{65}), e^{\pi \sqrt{190/12}} = (2 \sqrt{2} + \sqrt{10}) (3 + \sqrt{10}),\\[2mm] \pi &=& \frac{12}{\sqrt{130}} \log \left\{\frac{(2 + \sqrt{5})(3 + \sqrt{13})}{\sqrt{2}}\right\},\\[2mm] \pi&=& \frac{24}{\sqrt{142}} \log \left\{\sqrt{\left(\frac{10 + 11 \sqrt{2}}{4}\right)} + \sqrt{\left(\frac{10 + 7 \sqrt{2}}{4}\right)}\right\},\\[2mm] \pi &=& \frac{12}{\sqrt{190}} \log \{(2 \sqrt{2} + \sqrt{10}) (3 + \sqrt{10})\}, \\[2mm] \pi &=& \frac{12}{\sqrt{310}} \log [\frac{1}{4} (3 + \sqrt{5}) (2 + \sqrt{2}) \{( 5 + 2 \sqrt{10}) + \sqrt{(61 + 20 \sqrt{10})}\}],\\[2mm] \pi &=& \frac{4}{\sqrt{522}} \log \left[\left(\frac{5 + \sqrt{29}}{\sqrt{2}}\right)^3 (5 \sqrt{29} + 11 \sqrt{6})\right.\\[2mm] &&\left. \times \left\{ \sqrt{\left(\frac{9+3 \sqrt{6}}{4}\right)} + \sqrt{\left(\frac{5+3 \sqrt{6}}{4}\right)}\right\}^6 \right]. \end{eqnarray*} The last five formulæ are correct to 15, 16, 18, 22 and 31 places of decimals respectively.

8. Thus we have seen how to approximate to $\pi$ by means of logarithms of surds. I shall now shew how to obtain approximations in terms of surds only. If $$ n \frac{K'}{K} = \frac{L'}{L} , $$ we have $$ \frac{ndk}{kk'^2 K^2} = \frac{dl}{ll'^2 L^2}.$$ But, by means of the modular equation connecting $k$ and $l$, we can express $dk/dl$ as an algebraic function of $k$, a function moreover in which all coefficients which occur are algebraic numbers. Again, $$ q = e^{-\pi K'/K}, q^n = e^{-\pi L'/L},$$

Differentiating this equation logarithmically, and using the formula $$\frac{dq}{dk} = \frac{\pi^2 q}{2kk'^2 K^2}, $$ we see that where $A(k)$ denotes an algebraic function of the special class described above. I shall use the letter $A$ generally to denote a function of this type. Now, if we put $k=l'$ and $k'=l$ in (16), we have

The algebraic function $A(k)$ of course assumes a purely numerical form when we substitute the value of $k$ deduced from the modular equation. But by substituting $k=l'$ and $k'=l$ in (15) we have \begin{eqnarray*} && n^{\frac{1}{4}} e^{-\pi \sqrt{n}/12} (1- e^{-2 \pi \sqrt{n}}) (1- e^{-4 \pi \sqrt{n}}) (1 - e^{-6 \pi \sqrt{n}})\cdots\\ &=& e^{-\pi/(12 \sqrt{n})} (1- e^{-2\pi/\sqrt{n}}) (1- e^{-4 \pi/\sqrt{n}}) (1 - e^{- 6\pi/\sqrt{n}})\cdots \end{eqnarray*} Differentiating the above equation logarithmically we have

Now, adding (17) and (18), we have But it is known that $$ 1 -24 \left(\frac{q}{1+q} + \frac{3q^3}{1+q^3} + \frac{5q^5}{1+q^5} + \cdots \right) = \left(\frac{2K}{\pi}\right)^2 (1-2k^2), $$ so that Hence, dividing (19) by (20), we have where $R$ can always be expressed in radicals if $n$ is any rational number. Hence we have nearly, the error being about $8 \pi e^{-\pi \sqrt{n}} (\pi \sqrt{n}-3).$

9. We may get a still closer approximation from the following results. It is known that $$ 1 + 240 \sum^{r=\infty}_{r=1} \frac{r^3 q^{2r}}{1-q^{2r}} = \left(\frac{2K}{\pi}\right)^4 (1- k^2 k'^2), $$ and also that $$ 1-504 \sum^{r=\infty}_{r=1} \frac{r^5q^{2r}}{1-q^{2r}} = \left(\frac{2K}{\pi}\right)^6 (1-2K^2) (1+\frac{1}{2} k^2 k'^2).$$ Hence, from (19), we see that

where $R'$ can always be expressed in radicals for any rational value of $n$. Hence nearly, the error being about $24 \pi (10 \pi \sqrt{n} - 31) e^{-2 \pi \sqrt{n}}$ It will be seen that the error in (24) is much less than that in (22), if $n$ is at all large.

10. In order to find $R$ and $R'$ the series in (16) must be calculated in finite terms. I shall give the final results for a few values of $n$.

$$q= e^{-\pi K'/K}, q^n = e^{-\pi L'/L},$$ $$ f (q) = n \left(1-24 \sum^\infty_1 \frac{q^{2mn}}{1-q^{2mn}} \right) - \left(1-24 \sum^\infty_1 \frac{q^{2m}}{1-q^{2m}}\right), $$ \begin{eqnarray*} f(2) &=& \frac{4KL}{\pi^2} (k' + l), \\[2mm] f(3) &=& \frac{4KL}{\pi^2} (1 + kl + k'l'),\\[2mm] f(4) &=& \frac{4KL}{\pi^2} (\sqrt{k'} + \sqrt{l})^2, \\[2mm] f(5) &=& \frac{4KL}{\pi^2} (3 + kl + k'l') \sqrt{\left(\frac{1+kl+k'l'}{2}\right)}, \\[2mm] f(7) &=& \frac{12KL}{\pi^2} (1 + kl + k'l'),\\[2mm] f(11) &=& \frac{8KL}{\pi^2} \{2(1+kl+k'l') + \sqrt{(kl)} + \sqrt{(k'l')} - \sqrt{(kk'll')}\}, \\[2mm] f(15) &=& \frac{4KL}{\pi^2} [\{1+(kl)^{\frac{1}{4}} + (k'l')^{\frac{1}{4}}\}^4 - \{1+kl+k'l'\}],\\[2mm] f(17) &=& \frac{4KL}{\pi^2} \sqrt{}\{44 (1+ k^2 l^2 + k'^2 l'^2) + 168(kl +k'l' - kk'll') \\[2mm] && - 102 (1-kl-k'l')(4kk'll')^{\frac{1}{3}} - 192(4kk'll')^{\frac{2}{3}}\},\\[2mm] f(19) &=& \frac{24KL}{\pi^2} \{(1+ kl+k'l')+\sqrt{(kl)} + \sqrt{(k'l')} - \sqrt{(kk'll')}\},\\[2mm] f(23) &=& \frac{4KL}{\pi^2} [11(1+kl+k'l') -16(4kk'll')^{\frac{1}{6}} \{1+\sqrt{(kl)} + \sqrt{(k'l')}\} -20 (4kk'll')^{\frac{1}{3}}],\\[2mm] f(31) &=& \frac{12KL}{\pi^2} [3 (1+kl+k'l') + 4 \{\sqrt{(kl)} + \sqrt{(k'l')} + \sqrt{(kk'll')}\}\\[2mm] &&- 4 (kk'll')^{\frac{1}{4}} \{1+(kl)^{\frac{1}{4}} + (k'l')^{\frac{1}{4}}\}],\\[2mm] f(35) &=& \frac{4KL}{\pi^2} [2 \{\sqrt{(kl)} + \sqrt{(k'l')} - \sqrt{(kk'll')}\}\\[2mm] &&+(4kk'll')^{-\frac{1}{6}} \{1-\sqrt{(kl)} - \sqrt{(k'l')}\}^3]. \end{eqnarray*}

Thus the sum of the series (19) can be found in finite terms, when $n=2,3,4,5,\ldots,$ from the equations in Table III. We can use the same table to find the sum of (19) when $n=9,25,49,\ldots;$ but then we have also to use the equation $$ \frac{3}{\pi} = 1- 24 \left(\frac{1}{e^{2\pi}-1} + \frac{2}{e^{4\pi}-1} + \frac{3}{e^{6\pi}-1} + \cdots \right),$$ which is got by putting $k=k'=1/\sqrt{2}$ and $n=1$ in (18). Similarly we can find the sum of (19) when $n=21,33,57,93,\ldots,$ by combining the values of $f(3)$ and $f(7), f(3)$ and $f(11)$, and so on, obtained from Table III.

11. The errors in (22) and (24) being about $$ 8 \pi e^{-\pi \sqrt{n}} (\pi \sqrt{n}-3), 24 \pi (10 \pi \sqrt{n} - 31) e^{-2\pi \sqrt{n}}, $$ we cannot expect a high degree of approximation for small values of $n$. Thus, if we put $n=7,9,16,$ and 25 in (24), we get \begin{eqnarray*} \frac{19}{16} \sqrt{7} &=& 3.14180\ldots,\\[2mm] \frac{7}{3}\left(1+\frac{\sqrt{3}}{5}\right) &=& 3.14162\ldots,\\[2mm] \frac{99}{80} \left(\frac{7}{7-3\sqrt{2}}\right) &=& 3.14159274\ldots, \\[2mm] \frac{63}{25} \left(\frac{17+15\sqrt{5}}{7+15\sqrt{5}}\right) &=& 3.14159265380\ldots, \end{eqnarray*} while $$\pi = 3.14159265358 \ldots.$$ But if we put $n=25$ in (22), we get only $$\frac{9}{5} + \sqrt{\frac{9}{5}} = 3.14164\ldots.$$

12. Another curious approximation to $\pi$ is $$\left(9^2 + \frac{19^2}{22}\right)^{\frac{1}{4}} = 3.14159265262\ldots.$$ This value was obtained empirically, and it has no connection with the preceding theory. The actual value of $\pi$, which I have used for purposes of calculation, is $$\frac{355}{113} \left(1-\frac{.0003}{3533}\right)=3.1415926535897943\ldots,$$ which is greater than $\pi$ by about $10^{-15}$. This is obtained by simply taking the reciprocal of $1- (113 \pi/355)$. In this connection it may be interesting to note the following simple geometrical constructions for $\pi$. The first merely gives the ordinary value 355/113. The second gives the value $(9^2 + 19^2/22)^{\frac{1}{4}}$ mentioned above.

(1) Let $AB$ (Fig.1) be a diameter of a circle whose centre is $O$. Bisect $AO$ at $M$ and trisect $OB$ at $T$. Draw $TP$ perpendicular to $AB$ and meeting the circumference at $P$. Draw a chord $BQ$ equal to $PT$ and join $AQ$. Draw $OS$ and $TR$ parallel to $BQ$ and meeting $AQ$ at $S$ and $R$ respectively. Draw a chord $AD$ equal to $AS$ and a tangent $AC=RS$. Join $BC, BD,$ and $CD$; cut off $BE=BM,$ and draw $EX$, parallel to $CD$, meeting $BC$ at $X$.

Then the square on $BX$ is very nearly equal to the area of the circle, the error being less than a tenth of an inch when the diameter is 40 miles long.

(2)Let $AB$ (Fig.2) be a diameter of a circle whose centre is $O$. Bisect the arc $ACB$ at $C$ and trisect $AO$ at $T$. Join $BC$ and cut off from it $CM$ and $MN$ equal to $AT$. Join $AM$ and $AN$ and cut off from the latter $AP$ equal to $AM$. Through $P$ draw $PQ$ parallel to $MN$ and meeting $AM$ at $Q$. Join $OQ$ and through $T$ draw $TR$, parallel to $OQ$ and meeting $AQ$ at $R$. Draw $AS$ perpendicular to $AO$ and equal to $AR$, and join $OS$.

Then the mean proportional between $OS$ and $OB$ will be very nearly equal to a sixth of the circumference, the error being less than a twelfth of an inch when the diameter is 8000 miles long.

13. I shall conclude this paper by giving a few series for $1/\pi$. It is known that, when $ k \leq 1/\sqrt{2},$

Hence we have Differentiating both sides in (26) logarithmically with respect to $k$, we can easily shew that But it follows from (19) that, when $q = e^{-\pi \sqrt{n}}, n$ being a rational number, the left-hand side of (27) can be expressed in the form $$A \left(\frac{2K}{\pi}\right)^2 + \frac{B}{\pi},$$ where $A$ and $B$ are algebraic numbers expressible by surds. Combining (25) and (27) in such a way as to eliminate the term $(2K/\pi)^2$, we are left with a series for $1/\pi$. Thus, for example,

here $5 \sqrt{5}-1, 47 \sqrt{5} + 29, 89 \sqrt{5} + 59, \ldots $ are in arithmetical progression.

14. The ordinary modular equations express the relations which hold between $k$ and $l$ when $n K'/K = L'/L,$ or $q^n =Q$, where $$q = e^{-\pi K'/K}, Q=e^{-\pi L'/L},$$ $$K=1 + \left(\frac{1}{2}\right)^2 k^2 + \left(\frac{1\cdot3}{2\cdot4}\right)^2 k^4 + \cdots.$$ There are corresponding theories in which $q$ is replaced by one or other of the functions $$q_1 = e^{-\pi K_1' \sqrt{2}/K_1}, q_2 = e^{-2\pi K_2'/(K_2 \sqrt{3})}, q_3 = e^{-2\pi K_3'/K_3},$$ where \begin{eqnarray*} K_1 &=& 1+\frac{1\cdot3}{4^2} k^2 + \frac{1\cdot3\cdot5\cdot7}{4^2\cdot8^2} k^4 + \frac{1\cdot3\cdot5\cdot7\cdot9\cdot11}{4^2\cdot8^2\cdot12^2} k^6+ \cdots,\\[2mm] K_2 &=& 1+\frac{1\cdot2}{3^2} k^2 + \frac{1\cdot2\cdot4\cdot5}{3^2\cdot6^2} k^4+ \frac{1\cdot2\cdot4\cdot5\cdot7\cdot8}{3^2\cdot6^2\cdot9^2} k^6 + \cdots\\[2mm] K_3 &=& 1+\frac{1\cdot5}{6^2} k^2 + \frac{1\cdot5\cdot7\cdot11}{6^2\cdot12^2} k^4 + \frac{1\cdot5\cdot7\cdot11\cdot13\cdot17}{6^2\cdot12^2\cdot18^2} k^6 + \cdots . \end{eqnarray*} From these theories we can deduce further series for $1/\pi$, such as

In all these series the first factors in each term form an arithmetical progression; e.g. 2, 17, 32, 47, $\ldots$, in (31), and 4, 37, 70, 103, $\ldots$ , in (32). The first two series belong to the theory of $q_2$, the next two to that of $q_3$, as the rest to that of $q_1$. The last series (44) is extremely rapidly convergent. Thus, taking only the first term, we see that $$\frac{1103}{99^2}= .11253953678\ldots,$$ $$\frac{1}{2\pi\sqrt{2}}=.11253953951\ldots .$$

15. In concluding this paper I have to remark that the series $$1-24 \left(\frac{q^2}{1-q^2} + \frac{2q^4}{1-q^4} +\frac{3q^6}{1-q^6} + \cdots \right),$$ which has been discussed in $\S\S$ 8-13, is very closely connected with the perimeter of an ellipse whose eccentricity is $k$. For, if $a$ and $b$ be the semi-major and the semi-minor axes, it is known that

where $p$ is the perimeter and $k$ the eccentricity. It can easily be seen from (45) that But, taking the equation $$q^{\frac{1}{12}} (1-q^2) (1-q^4) (1-q^6) \cdots = (2kk')^{\frac{1}{6}} \sqrt{(K/\pi)},$$ and differentiating both sides logarithmically with respect to $k$, and combining the result with (46) in such a way as to eliminate $dK/dk$, we can shew that But we have shewn already that the right-hand side of (47) can be expressed in terms of $K$ if $q=e^{-\pi \sqrt{n}},$ where $n$ is any rational number. It can also be shewn that $K$ can be expressed in terms of $\Gamma$-functions if $q$ be of the forms $e^{-\pi n},e^{-\pi n\sqrt{2}}$ and $e^{-\pi n \sqrt{3}}$, where $n$ is rational. Thus, for example, we have and so on.

The following approximations for $p$ were obtained empirically:

where $\epsilon$ is about $ak^{12}/1048576 $; where $\epsilon$ is about $3ak^{20} / 68719476736.$